BETONexpress è l'unico software per il progetto e la verifica di elementi strutturali in c.a allo stato limite ultimo (SLU) e allo stato limite di esercizio (SLE) con licenze permanenti e aggiornamenti gratuiti!!
BETONexpress è l'unico software per il progetto e la verifica di elementi strutturali in c.a allo stato limite ultimo (SLU) e allo stato limite di esercizio (SLE) con licenze permanenti e aggiornamenti gratuiti!!
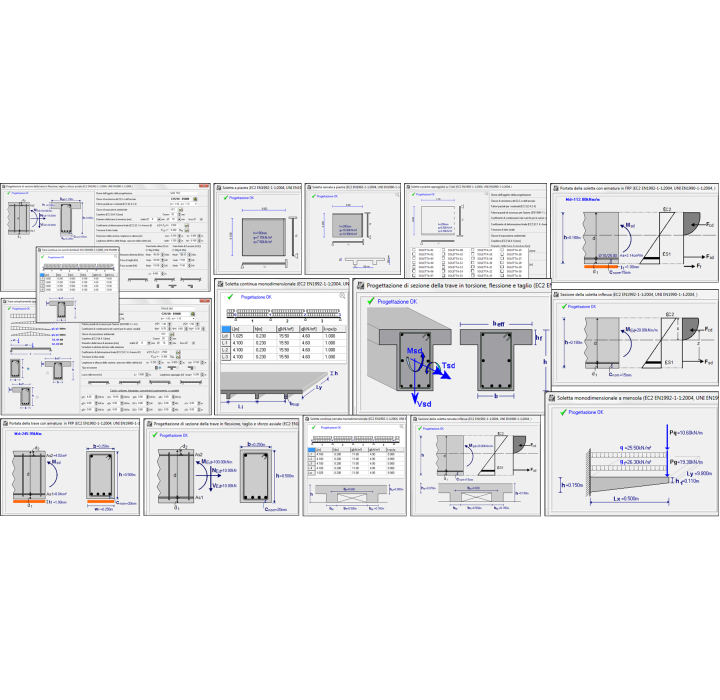
Con BETONexpress è possibile progettare facilmente elementi strutturali in c.a.: per ogni elemento si definiscono le dimensioni, i carichi e le proprietà dei materiali e si ottiene il progetto dettagliato con una relazione di calcolo dettagliata unito a una distinta dei ferri automatica. Il programma genera automaticamente i disegni dettagliati della struttura e dell’armatura.
Il dimensionamento è eseguito secondo l’Eurocodice 2, EN 1992-1-1:2004, Design of concrete structures, General rules and rules for buildings, con integrazione dell’Eurocodice 7, EN 1997-1:2004, Geotechnical design – General rules, for geotechnical analysis (footings, retaining walls), Eurocodice 0, EN 1990:2002, per le combinazioni di carico, e Eurocodice 8 per i carichi sismici. L’utente può scegliere gli Annessi Nazionali applicabili.
Caratteristiche del Software
- Licenze permanenti e aggiornamenti gratuiti
- Gran numero di strutture calcolabili
- Input dati estrememente semplice
- Risultati immediati
- Ogni verifica riporta il riferimento di normativa
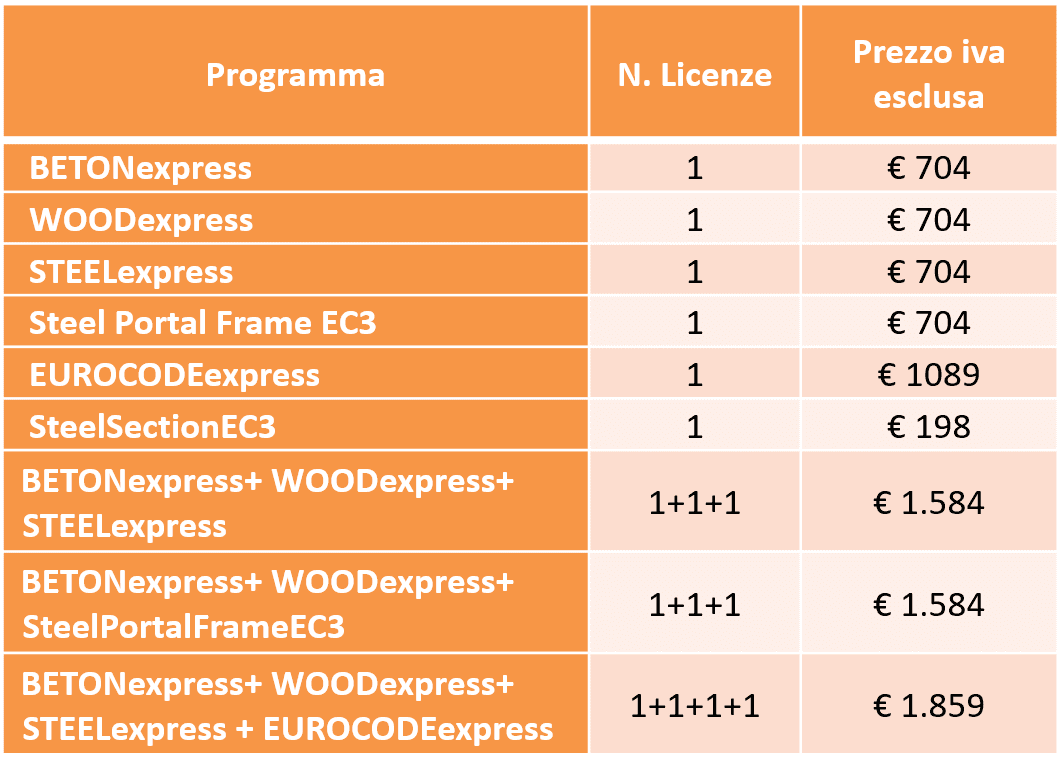
Listino prezzi e offerte
licenze permanenti + aggiornamenti gratuiti
Per i clienti dei programmi WOODexpress, BETONexpress e STEELexpress è previsto uno sconto sull'acquisto di EUROCODEexpress: richiedi preventivo personalizzato
Contattateci per più licenze, vi manderemo un preventivo personalizzato
Tutti i programmi sono disponibili tramite download, incluso Help on line e manuale utente.
Per scuole, università e istituzioni contattateci
AGGIORNAMENTI
Gli aggiornamenti sono generalmente gratuiti, disponibili dal menu principale del programma "Update". Solo quando vengono sviluppati aggiornamenti importanti come cambiamenti agli Eurocodici o alle Normative, o quando sono aggiunte nuove funzionalità, verranno rilasciati aggiornamenti a pagamento, in genere al 20-30% del prezzo originale.
SERVIZI
Supporto tecnico gratuito direttamente dalla ditta produttrice RUNET(TM) Norway as.
Non vengono richiesti canoni di manutenzione.
PIASTRE - SOLETTE LISCE E NERVATE
- Carichi uniformemente distribuiti permanenti e accidentali. Combinazioni di carico secondo l'Eurocodice 0.
- Piastre bidimensionali con varie condizioni di appoggio. Metodi di analisi: Czerny, Bares o Marcus.
- Piastre continue mono-dimensionali (fino a 8 campate). Possono essere definiti gli sbalzi alle estremità. Fattori di carico per ogni campata. Ridistribuzione del momento.
- Piastre a sbalzo.
- Verifica di apertura fessure e deformabilità .
- Calcestruzzo normale o alleggerito.
- Resistenza a flessione delle sezioni delle piastre di calcestruzzo, anche rinforzate con FRP (polimeri fibro-rinforzati).
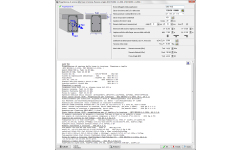
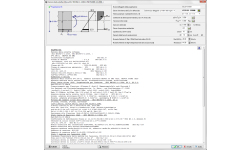
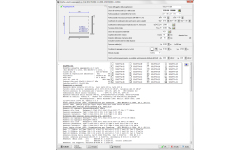
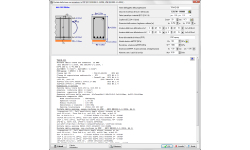
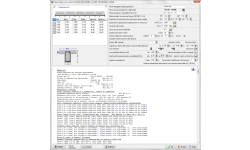
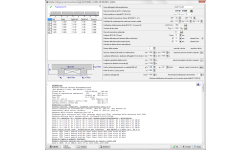
Piastre piane, Punzonamento

Sezione piastra a taglio-punzonamento
Progetto della sezione della piastra a taglio-punzonamento secondo l’Eurocodice 2 6.4. Verifica della capacità a taglio nel perimetro di verifica attorno ad un pilastro rettangolare. Se il taglio di progetto Ved supera la capacità a taglio Vrd,c, il programma calcola l’armatura a taglio necessaria (staffe).
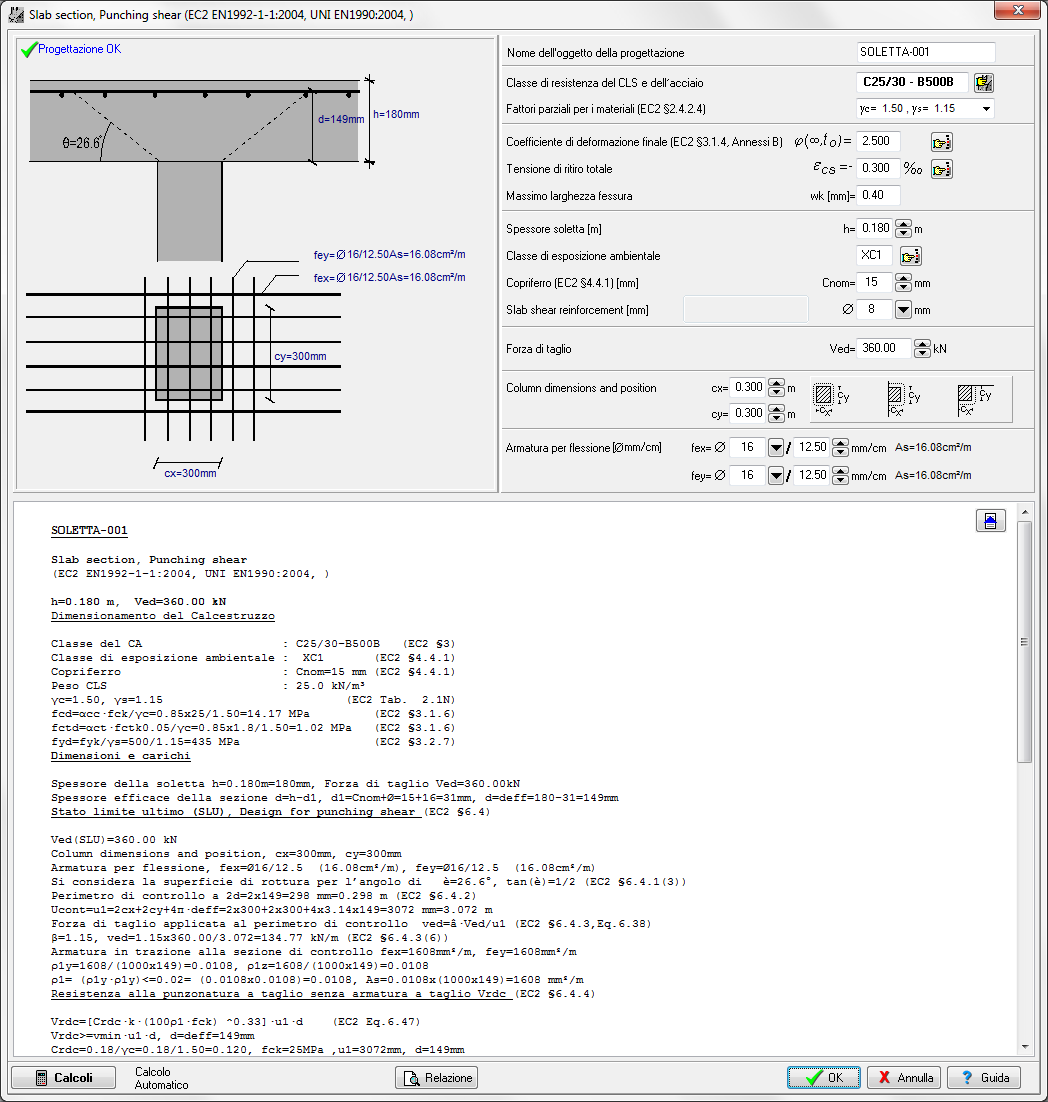
Valori di input.
Sforzo di taglio Ved sulla superficie del pilastro.
- Armatura longitudinale sul pilastro, nelle direzioni x e y.
- Specificare con Si o No se si vuole usare l’armatura a taglio o no. Se Si allora verrà calcolata l’armatura a taglio appropriata se lo sforzo di taglio βVed>Vrd,c.
- Dimensioni pilastro
- Posizione pilastro (interno, di bordo o d’angolo).
Armatura a taglio-punzonamento.
Se si sceglie l’opzione No per l’armatura a taglio si verifica che il punzonamento sia βVed<=Vrd,c. Se questa condizione non è soddisfatta viene mostrato il messaggio di aumentare lo spessore della piastra. Se si sceglie l’opzione SI per l’armatura a taglio, allora si calcola l’armatura perimetrale attorno ai pilastri.
Per l’armatura si usa il diametro selezionato. Se non è sufficiente, si seleziona un diametro maggiore.
Per l’armatura a taglio il numero minimo di perimetri è 3.
La spaziatura radiale delle staffe non supera 0.75d.
La spaziatura tangenziale delle staffe non supera 1.5d entro la distanza 2d dalla superficie del pilastro.
Il primo perimetro a taglio è ad una distanza <0.35d dalla superficie del pilastro.
L’ultimo perimetro è ad una distanza 1.5d all’interno del perimetro esterno dove l’armatura a taglio non è più richiesta. Eurocodice 2 Eq. 6.54. e Fig. 6.22
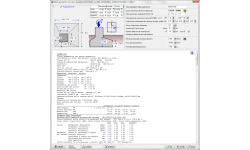
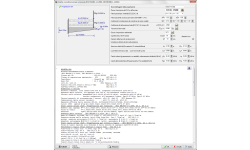
PROGETTO Piastre piane
Progetto di piastre piane con dimensioni di campata più interne Lx Ly, e dimensioni di campata alle estremità Lx’ e Ly’.
Specificare Si o No se si vuole usare l’armatura a taglio. Se si seleziona il Si, allora viene calcolata l’armatura a taglio appropriata se lo sforzo di taglio βVed>Vrd,c.
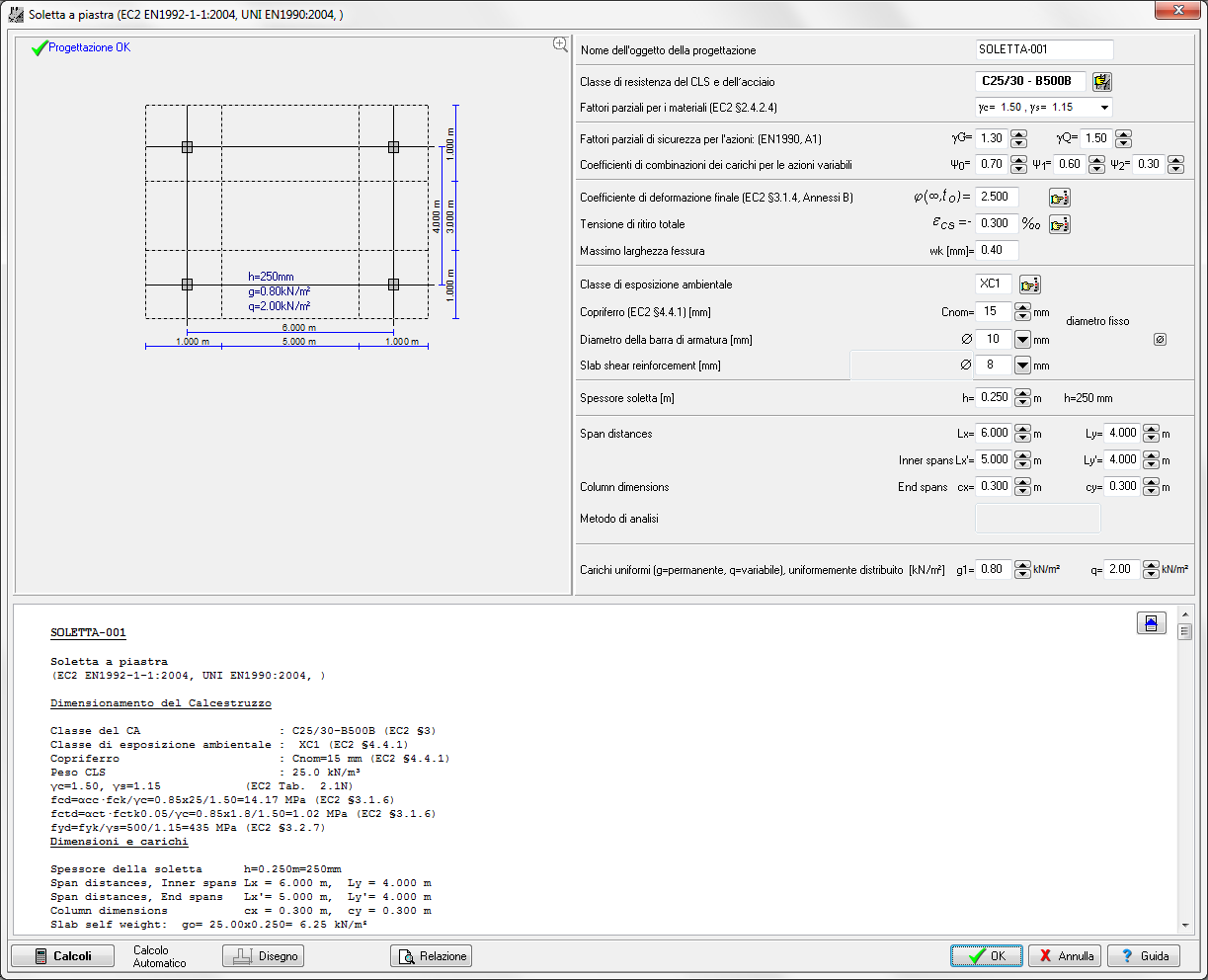
Analisi
L’analisi per il momento e lo sforzo di taglio si basa sui coefficienti delle travi continue.
Metodo 1:
Campate più interne
Momenti all’appoggio: Ms= (0.083·γG·g+0.111·γq·q)·L2/8
Momenti in campata: Mf= (0.063·γG·g+0.075·γq·q)·L2/8.
Campate di estremità
Momenti all’appoggio: Ms= (0.125·γG·g+0.125·γq·q)·L2/8
Momenti in campata: Mf= (0.080·γG·g+0.096·γq·q)·L2/8
Metodo 2:
Campate più interne
Momenti all’appoggio: Ms= (0.083·γGxg+0.083·γq·q)·L2/8
Momenti in campata: Mf= (0.063·γGxg+0.063vγq·q)·L2/8.
Campate di estremità
Momenti all’appoggio: Ms= (0.111·γG·g+0.111·γq·q)·L2/8
Momenti in campata: Mf= (0.077·γG·g+0.077vγq·q)·L2/8
Metodo 3 Tabella 3.1 BS8110
Campate più interne
Momenti all’appoggio: Ms= (0.063·γG·g+0.063·γq·q)·L2/8
Momenti in campata: Mf= (0.063·γG·g+0.063·γq·q)·L2/8.
Campate di estremità
Momenti all’appoggio: Ms= (0.086·γG·g+0.086·γq·q)·L2/8
Momenti in campata: Mf= (0.086·γG·g+0.086·γq·q)·L2/8
I momenti flettenti all’appoggio sono ridotti di (1-cx/Lx) 2 e (1-cy/Ly) 2 per le direzioni x e y
I momenti flettenti in campata sono ridotti di (1-cx/Lx) e (1-cy/Ly) per le direzioni x e y
Sforzi di taglio
Pilastri d’angolo Ved=0.25·(Lx’+cx)·(Ly+cy);
Pilastri di bordo Ved=0.50·(Lx’+cx)·Ly;
Pilastri più interni Ved=1.25·Lx·Ly;
I momenti flettenti della piastra piana sono ripartiti tra Zona su pilastro e Zona centrale secondo l’Eurocodice 2 Annesso I, come segue:
Momenti negativi: Zona su pilastro 70%, Zona centrale 30%
Momenti positivi: Zona su pilastro 55%, Zona centrale 45%
La Zona su pilastro in entrambe le direzioni x e y è uguale al min(Lx,Ly)/2.
Armatura a taglio-punzonamento.
Se si seleziona No per l’armatura a taglio il punzonamento è verificato in modo che βVed<=Vrd,c. Se questa condizione non è soddisfatta viene mostrato il messaggio di aumentare lo spessore della piastra. Se si seleziona SI per l’armatura a taglio, allora si calcola l’armatura perimetrale attorno ai pilastri.
Per l’armatura si usa il diametro selezionato. Se non è sufficiente si seleziona un diametro maggiore.
Per l’armatura a taglio il numero minimo di perimetri è 3.
La spaziatura radiale delle staffe non supera 0.75d.
La spaziatura tangenziale delle staffe non supera 1.5d entro la distanza 2d dalla superficie del pilastro.
Il primo perimetro a taglio è ad una distanza <0.35d dalla superficie del pilastro.
L’ultimo perimetro è ad una distanza 1.5d all’interno del perimetro esterno dove l’armatura a taglio non è più richiesta. Eurocodice 2 Eq. 6.54. e Fig. 6.22
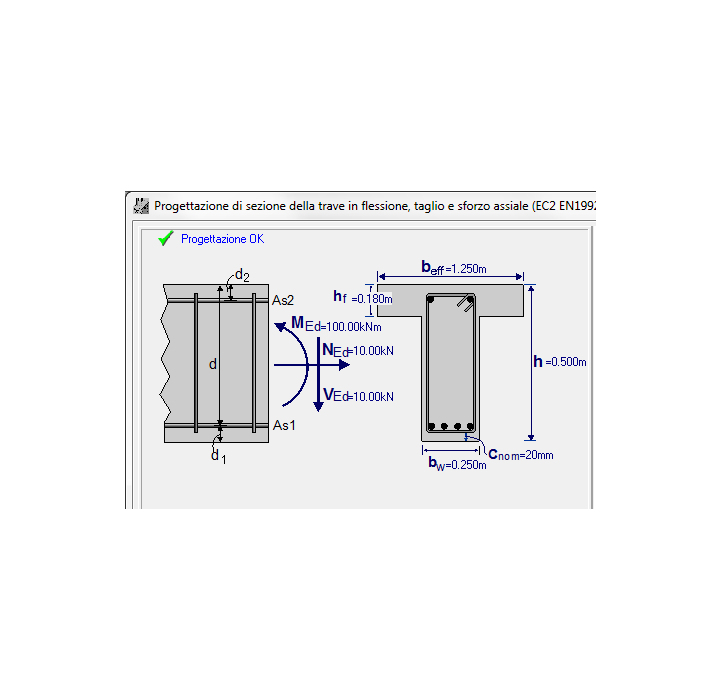
TRAVI a T e RETTANGOLARI
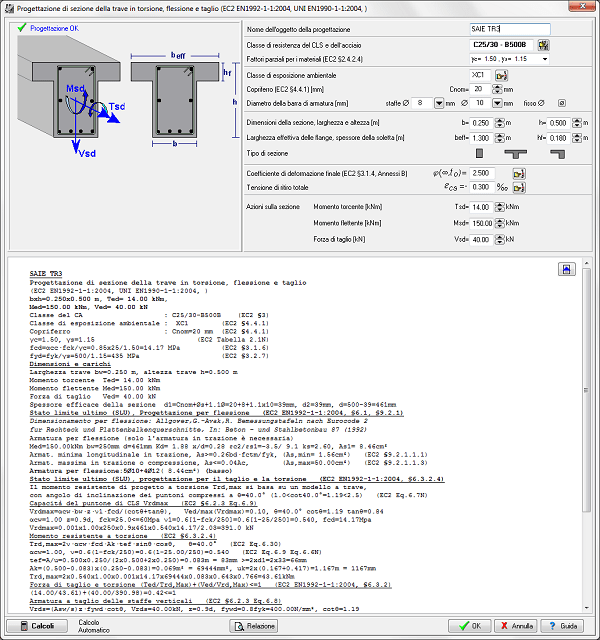
- Travi a T o rettangolari in combinazione di carico flessione taglio e forza assiale.
- Travi a campata singola sottoposte a combinazioni di carico.
- Travi continue (fino a 8 campate) sottoposte a carichi distribuiti uniformemente, combinazione di carico a flessione, taglio e torsione.
- Verifica di apertura fessure o deformabilità. New
- Calcestruzzo normale o alleggerito. New
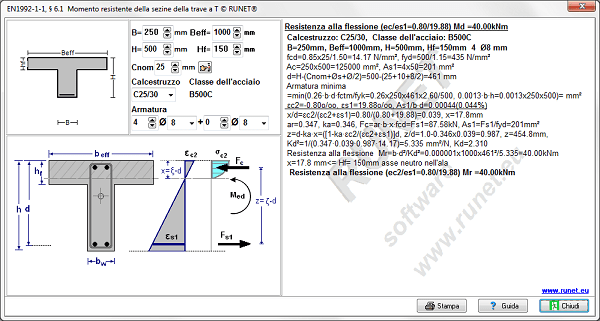
- Calcolo della resistenza a flessione delle sezioni delle travi, anche rinforzate con FRP (polimeri fibro-rinforzati).
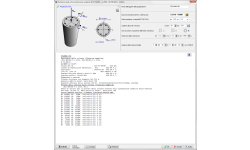
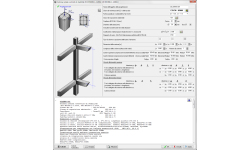
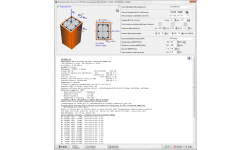
PILASTRI
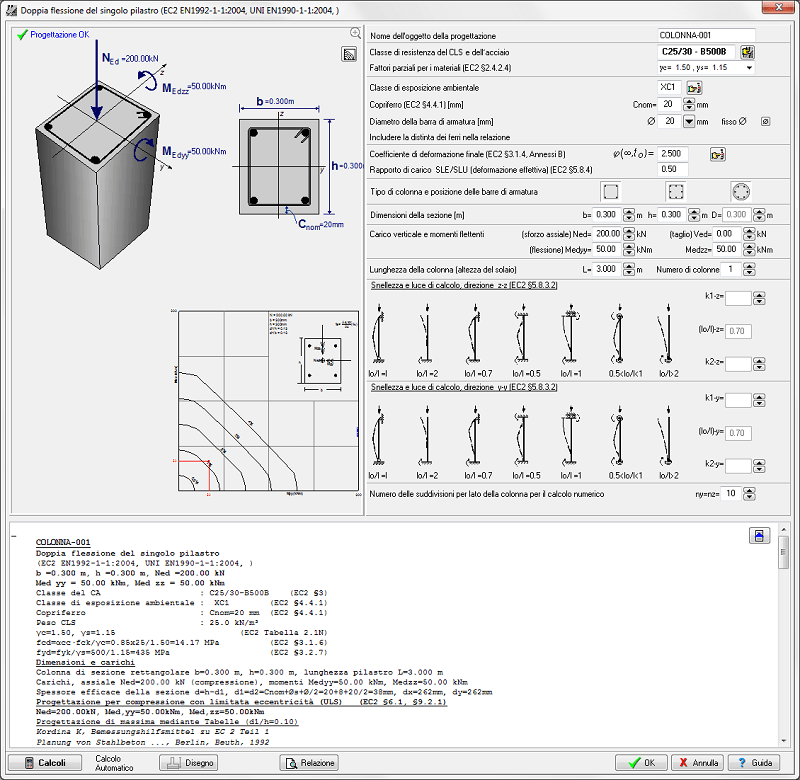
- Flessione biassiale, (sezioni rettangolari e circolari) pilastro isolato (verifica di instabilità). Effetti del secondo ordine.
- Flessione biassiale (N-Mx-My) diagrammi ottenuti da integrazione numerica delle forze del calcestruzzo e dell'acciaio sulla sezione.
- Calcolo della resistenza a momento delle sezioni dei pilastri in calcestruzzo, anche rinforzate con FRP (polimeri fibro-rinforzati).
- Diagrammi completi per flessione singola e biassiale. New
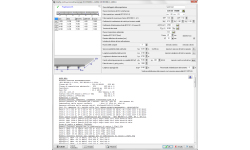
PLINTI DI FONDAZIONE
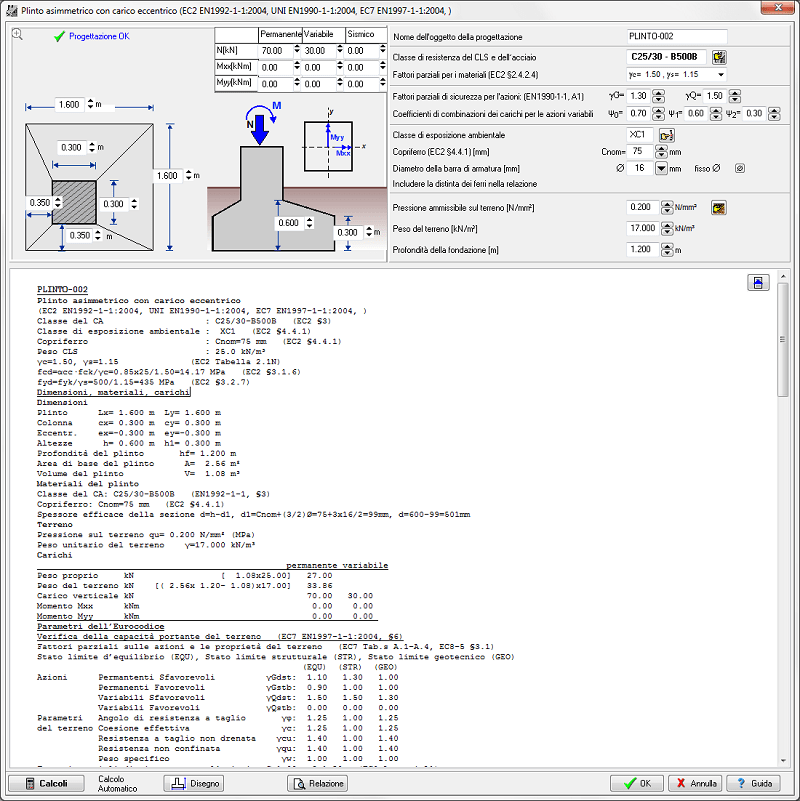
- Capacità portante delle Fondazioni (NEW!)
- Plinti caricati centralmente.
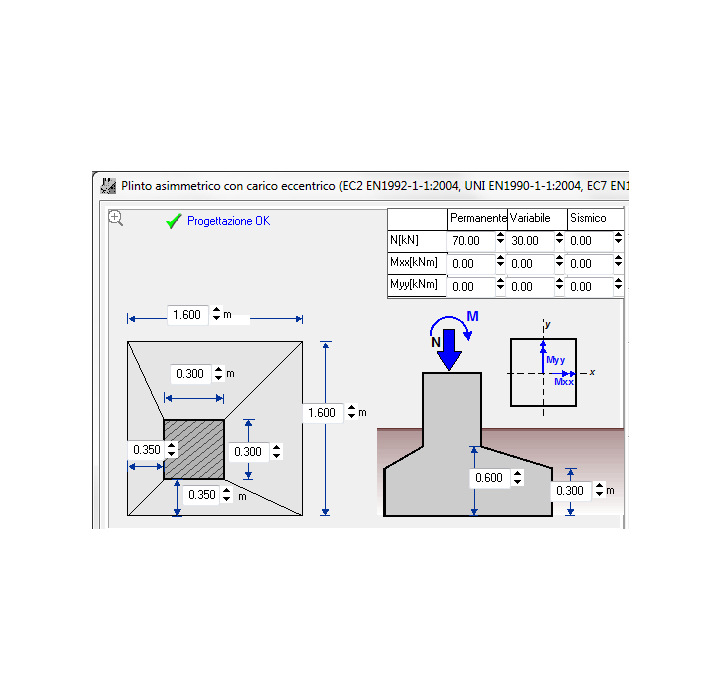
- Plinti con carichi eccentrici e plinti asimmetrici.
- Plinti per pilastri d’acciaio (NEW!)
Carico verticale e momenti sulla sommità. Carichi accidentali e permanenti.
Calcolo esatto della distribuzione della pressione sotto il piede. Progetto geotecnico secondo l'Eurocodice 7, EN 1997-1:2004, oppure progetto con calcolo delle tensioni ammissibili sul terreno.
Combinazioni di carico secondo l'Eurocodice 7 (combinazioni di carico EQU, STR, GEO) e l'Eurocodice 0.
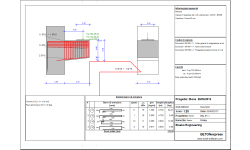
Disegno CAD completo del plinto con l'armatura.
Calcolo della capacità portante delle fondazioni per condizioni drenate e non drenate.
Si possono progettare Plinti per pilastri d’acciaio Incernierati o a Incastro.
Carichi sulle fondazioni, Tirante in acciaio alla base del pilastro e spinta passiva del terreno al lato della fondazione.
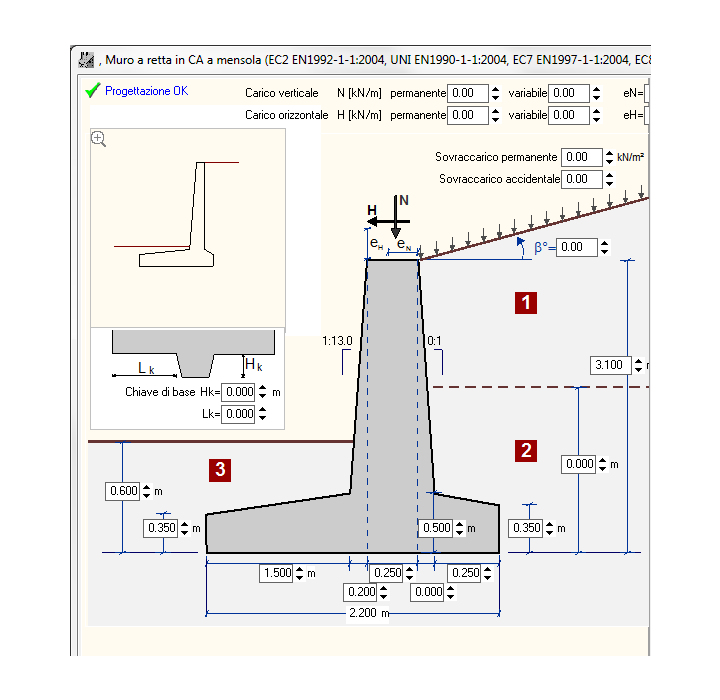
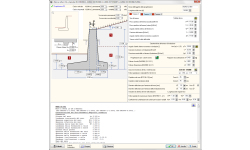
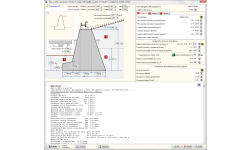
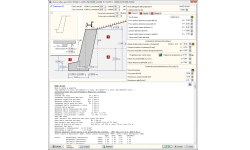
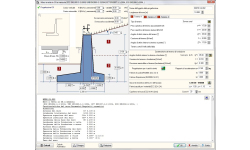
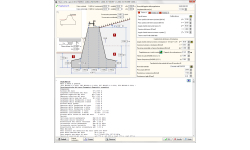
MURI DI CONTENIMENTO
- Muro a mensola
- Muro a retta a gravità
- Muro di ritegno
- Muro portante
- Pareti con carico orizzontale distribuito
- Serbatoi
Muri di contenimento a gravità o a mensola (con armatura).
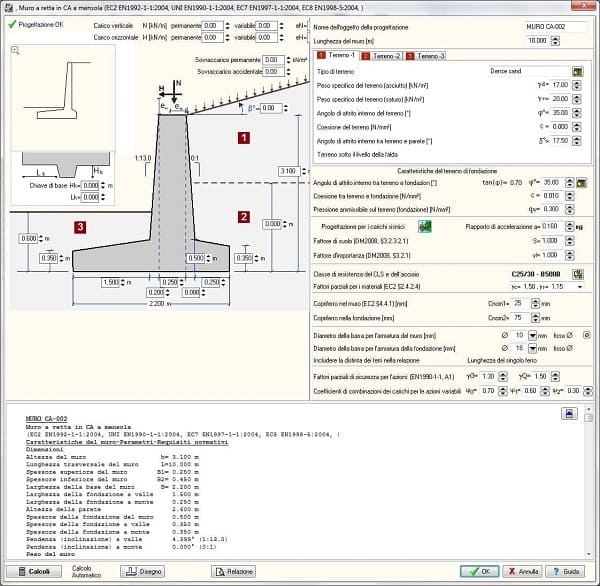
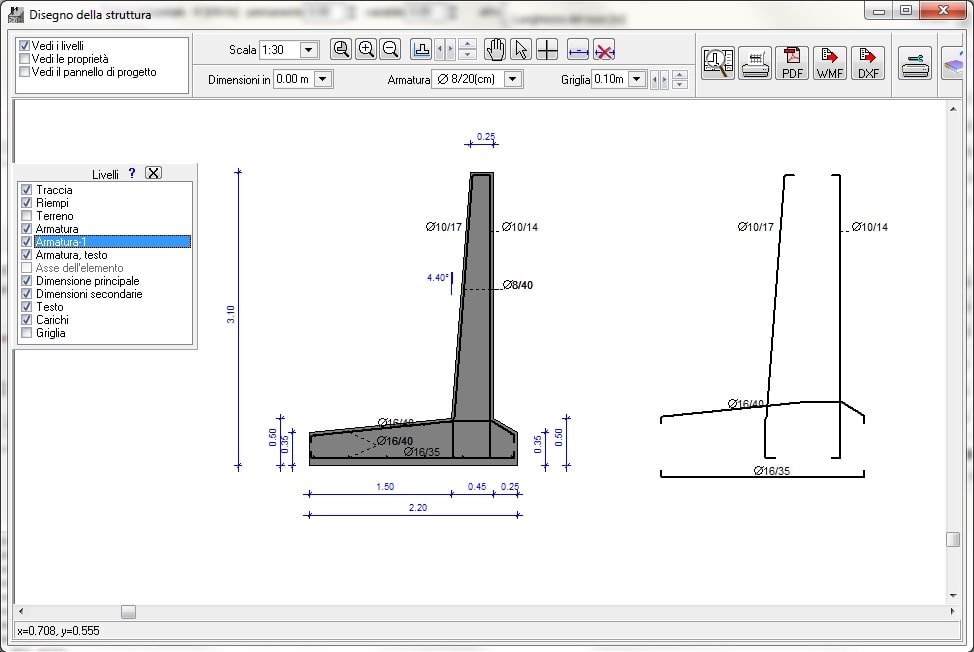
Progetto geotecnico secondo l’Eurocodice 7, EN 1997-1:2004, Progetto geotecnico – Calcolo agli stati limite oppure calcolo alle tensioni ammissibili sul terreno. Pressione al suolo attiva o passiva secondo la teoria di Coulomb. Progetto dei muri di gravità secondo l’Eurocodice 7 (EC7) o tensioni ammissibili.
Analisi sismica secondo l’Eurocodice 8 (EC8), Mononobe-Okabe.
Due tipi differenti di muri a mensola sono possibili nel programma:
- Tipo-A. Muri con ciabatta a monte molto piccola. La pressione attiva del terreno è calcolata usando la teoria di Coulomb nella superficie posteriore del muro.
- Tipo B. Muri con ciabatta a monte. La pressione attiva del terreno è calcolata usando la teoria di Rankine in una superficie verticale alla fine della ciabatta.
Il progetto del muro a mensola si basa sul Progetto di calcestruzzo agli Stati Limite Ultimi secondo l’Eurocodice 2.
I controlli del progetto sono eseguiti in una serie di sezioni lungo l’altezza della parete. L’armatura della parete è ottimizzata, e a seconda dell’altezza della parete l’armatura è ridotta verso la sommità del muro. I ferri sono automaticamente inseriti nella distinta dei ferri. Dente inferiore contro lo scorrimento.
Combinazione di carichi secondo l’Eurocodice 2, Eurocodice 7,( combinazioni di carico EQU, STR, GEO) e Eurocodice 0.
Disegno CAD completo del muro di contenimento con l’armatura.
Muri di ritegno
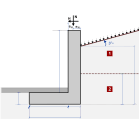
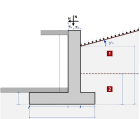
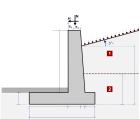
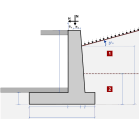
I muri di ritegno sono pareti fondate su zoccoli di fondazione. Ci sono due tipi di muri di ritegno:
- Muri con solo il fondo vincolato contro il movimento laterale,
- Muri con il fondo e la sommità vincolati contro il movimento laterale
Nel primo caso lo scorrimento della parete è evitato vincolando il movimento della base. La spinta attiva del terreno è calcolata usando le teorie di Coulomb(1776) o Rankine (1857). Eurocodice 7 9.5.1.
Nel secondo caso (quando anche la sommità della parete è vincolata contro il movimento laterale), le condizioni della spinta attiva del terreno sono ottenute per Ko in condizioni a riposo secondo Jaky (1948), Eurocodice 7 9.5.2.
Muri portanti
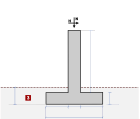
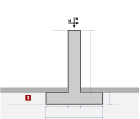
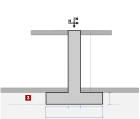
Muri portanti con carico verticale od orizzontale sulla sommità senza nessuna spinta del terreno.
Il carico orizzontale sulla sommità può essere definito dall’Eurocodice 1-1-1:2001 Tabella 6.12 secondo gli Annessi Nazionali, e l’uso del valore comune nelle costruzioni qk~ 0.50 - 1.00 (kN/m)Il carico orizzontale sulla sommità può essere definito anche secondo l’Eurocodice 1-1-7:2006, nel caso di carico d’impatto.
Pareti con carico orizzontale distribuito
In caso di carico vento, la spinta del vento è secondo l’Eurocodice1-1-4:2005.
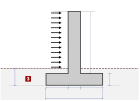
In caso di carico vento, la spinta del vento è secondo l’Eurocodice1-1-4:2005
qw = 0.001·Cpe·Cz(0)·0.625·vb2, (kN/m2)
Cpe: coefficiente di spinta per pareti verticali,
secondo la Tabella 7.1 EN1991-1-1,
Cpe = +0.80 (pressione) sulla superficie anteriore della parete
Cpe = -1.20 (depressione) sulla superficie posteriore della parete
Cz(0) coefficiente di esposizione, a seconda del terreno. Per vari terreni secondo la 1991-1-1 4.5 al livello del suolo Cz(0) è tra 1.20 e 2.00.
Vb è la velocità del vento di base in m/sec. Questo valore è dato nell’Annesso Nazionale dell’Eurocodice 1-1-4, per le varie regioni di un Paese. Valori comuni di Vb sono tra 25 e 40 m/s.
Così un calcolo del carico vento su un pannello è circa
qw~0.001x(0.80+1.20)x2.0x0.625x30.02~ 2.25 kN/m2
Serbatoi
Il progetto è per Serbatoi rettangolari. La soluzione è per una sezione bidimensionale lungo la dimensione minore (larghezza) del serbatoio.
Le condizioni di carico includono tutti i casi di carico secondo l’Eurocodice 0, (EQU, STR e GEO) per:
· Serbatoio vuoto (solo spinta del terreno)
· Serbatoio pieno senza spinta del terreno
· Serbatoio pieno con spinta del terreno
Il progetto del cemento armato include anche la verifica di esercizio, con apertura delle fessure limite specificato dall’utente.
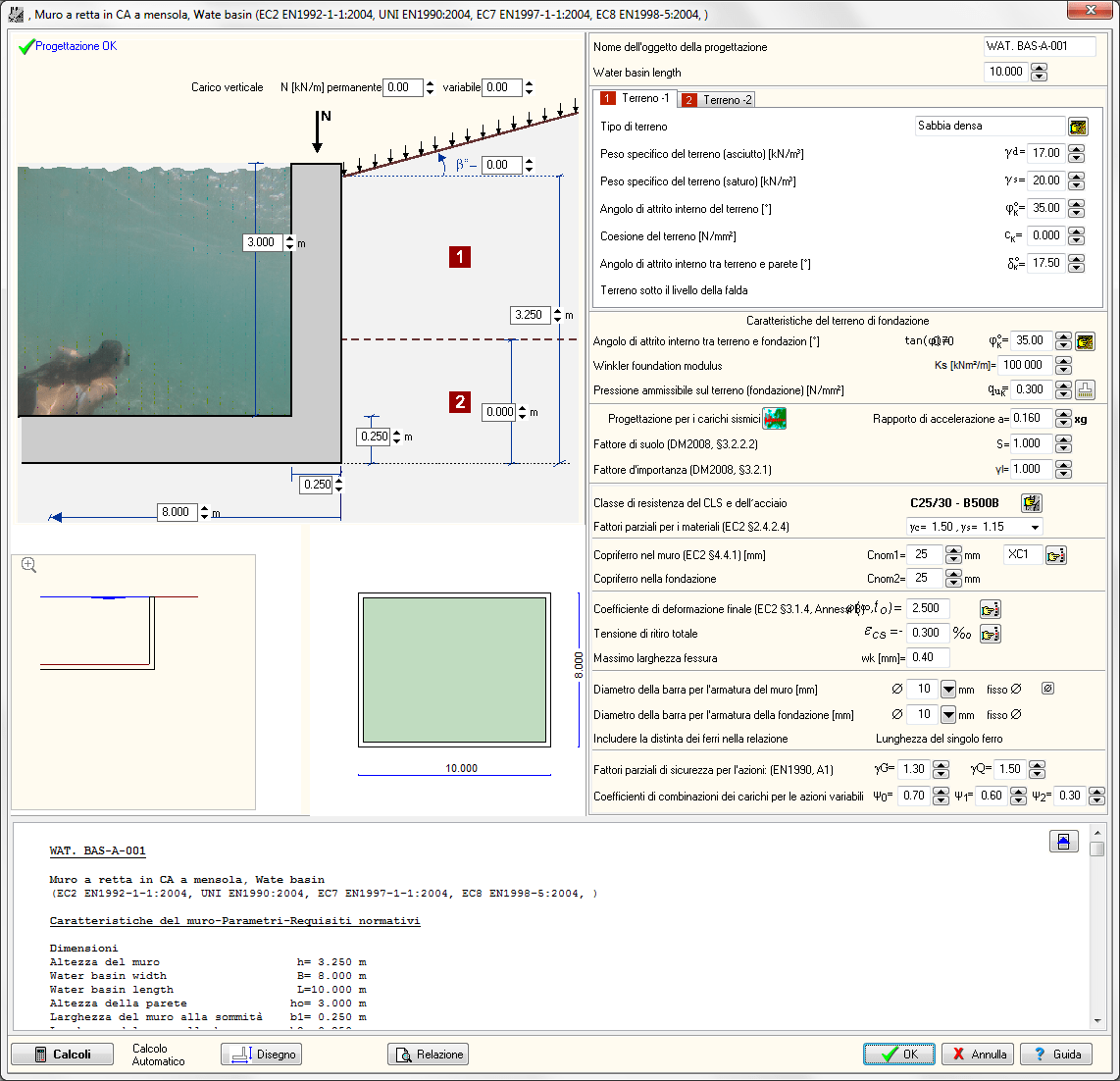
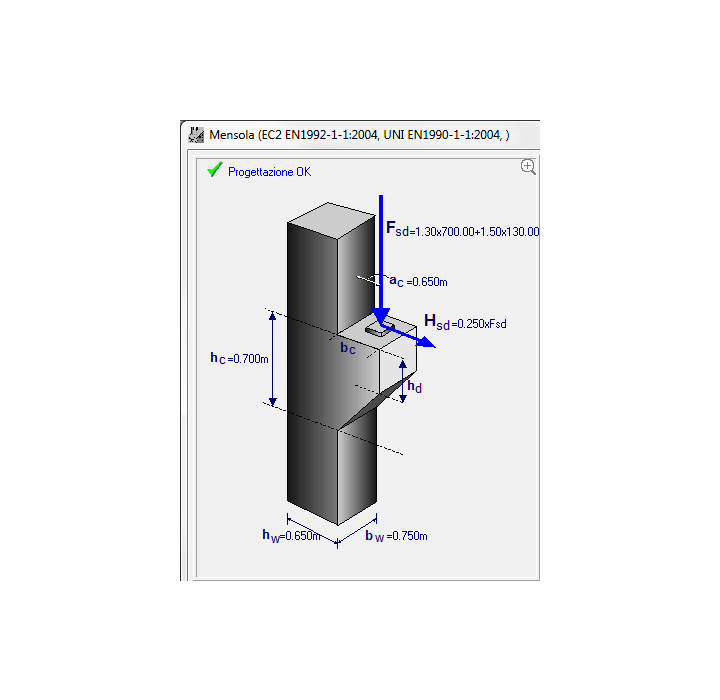
MENSOLE
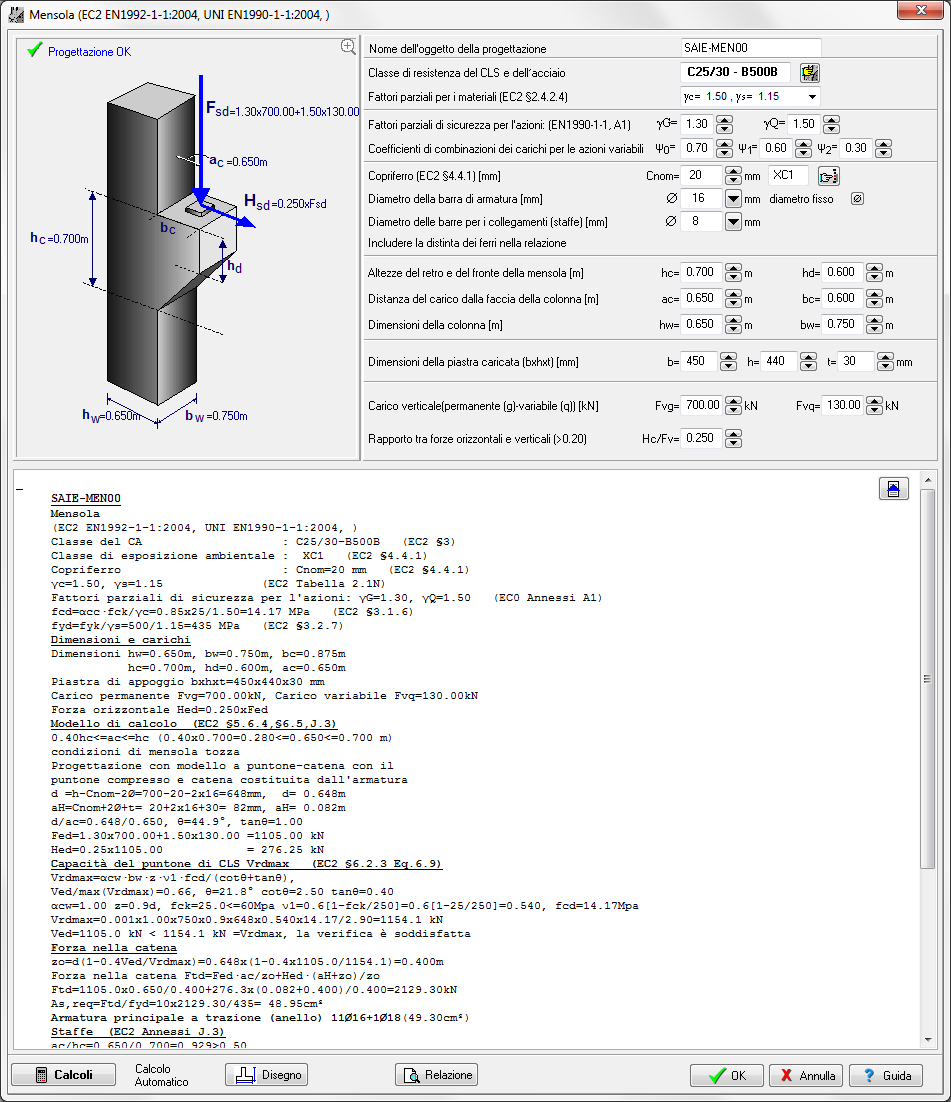
Mensole corte sporgenti dalle facce dei pilastri, aventi rapporto ac/hc<=1, dove ac è il braccio della forza e hc l’altezza della mensola. Progetto secondo l’Eurocodice 2 §2.5.3.7. Combinazione di carichi secondo l’Eurocodice 2 e l’Eurocodice 1.
Disegno CAD completo della mensola con l’armatura.
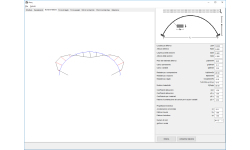
TRAVE TOZZA
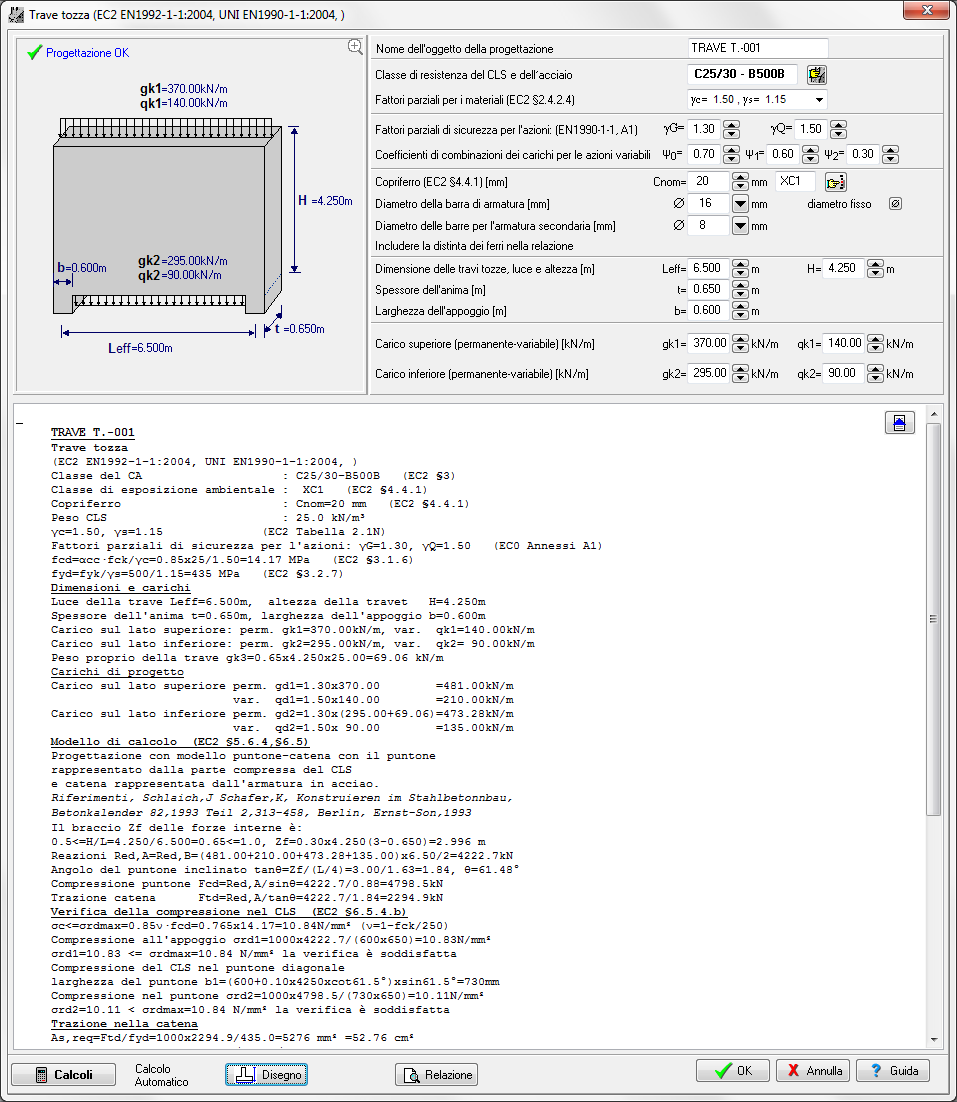
Travi tozze con dimensione Leff / h <= 2, dove Leff è la lunghezza e h l’altezza.
Progetto secondo l’Eurocodice 2, §5.6.4,§6.5, usando il modello strut and tie. Si possono progettare travi tozze soggette a carichi distribuiti uniformemente (con componenti accidentali e permanenti) sulle facce superiore e inferiore della trave.
Combinazioni di carichi secondo l’Eurocodice 2 e l’Eurocodice 0.
Disegno CAD completo della trave con l’armatura.
Le base per il progetto delle fondazioni è la capacità portante del terreno.

La capacità portante di progetto può essere calcolata usando il metodo analitico o quello semi-empirico. L’Annesso D dell’Eurocodice 7 EN1997:2004 descrive un metodo per ottenere la resistenza di progetto del terreno.
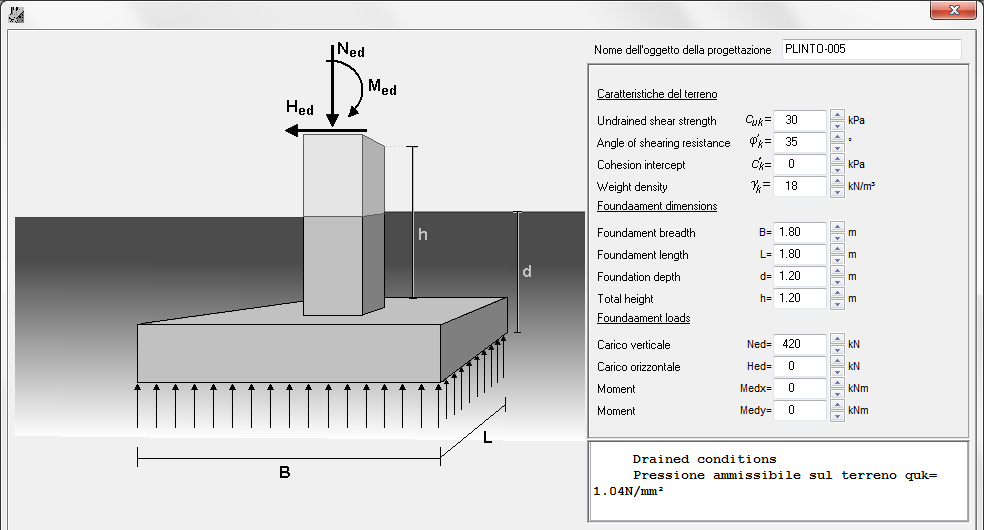
I metodi dell’Annesso D per condizioni drenate e non drenate sono implementati nel programma.
La portata di progetto del terreno è calcolata per condizioni EQU, STR e GEO.
Il calcolo della portata di progetto è per condizioni drenate e non drenate del suolo. Per condizioni drenate del terreno le proprietà importanti del suolo sono l’ Angolo di attrito φk [°] e la Coesione efficace c [kPA]. Per condizioni non drenate del terreno la proprietà importante del suolo è Resistenza al taglio non drenata cu [kPa].
Per il calcolo della portata di progetto altri parametri sono le dimensioni e l’altezza della fondazione del plinto, così come i carichi e le eccentricità dei carichi.
Nel programma, per il progetto della fondazione, per la resistenza del terreno usiamo la tensione di compressione sul terreno quk (N/mm2). Cioè una resistenza del terreno corrispondente alla pressione ammissibile del terreno. Nel progetto della fondazione usiamo come tensione di compressione sul terreno di progetto qud = quk/γqu, dove γqu è il fattore parziale per la resistenza non confinata. (Eurocodice 7, Annesso A). Quindi per essere consistenti la resistenza di progetto calcolata dall’Annesso D dell’Eurocodice7 con la tensione di compressione sul terreno usata nel programma, il valore di progetto deve essere moltiplicato per γqu.
È γqu =1.40 per EQU e 1.00 e 1.4 per (STR-GEO).
Cliccare  nel progetto delle fondazioni o nel progetto dei muri di sostegno, e si apre la finestra di calcolo della capacità portante di progetto.
nel progetto delle fondazioni o nel progetto dei muri di sostegno, e si apre la finestra di calcolo della capacità portante di progetto.
Dai parametri del terreno e delle fondazioni si ha il calcolo della resistenza portante del terreno quk che si può usare nel programma.
Se qui si spunta includi i calcolo nella relazione, allora la resistenza portante di progetto sarà impostata al minimo calcolato e i calcoli saranno inclusi nella relazione del progetto dei plinti. (ricorda che se vuoi cambiare le dimensioni o i carichi bisogna ricalcolare quk).
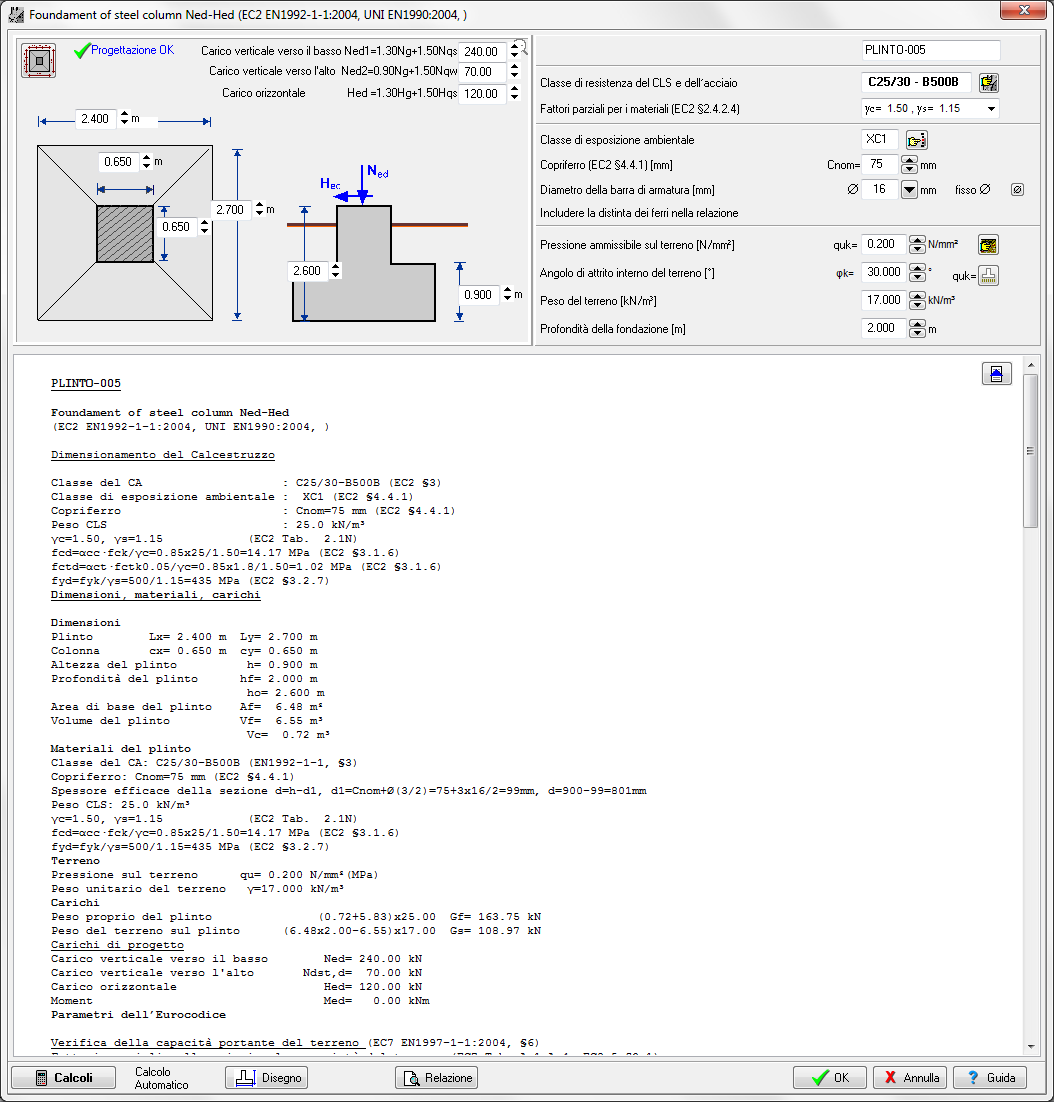
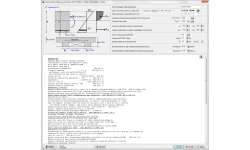
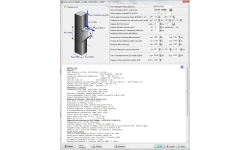
PLINTI PER PILASTRI D'ACCIAIO
Il plinto in calcestruzzo per strutture in acciaio deve essere progettato per assorbire la pressione del terreno per il massimo carico verticale e deve avere un peso sufficiente per assorbire la forza di sollevamento (vento o forze sismiche).
Si possono progettare fondazioni alla base dei pilastri Incernierate o a Incastro.
Si può anche specificare se la fondazione ha un tirante orizzontale per assorbire le forze orizzontali verso l’esterno o no.
Carichi sulle fondazioni: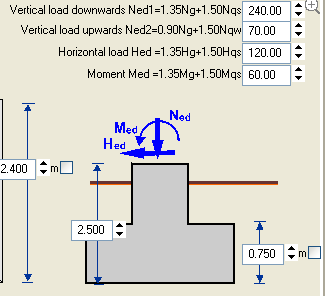
Le azioni finali dopo la moltiplicazione per il coefficiente di sicurezza (γG e γQ). Eurocodice-19990-1-1, Tab.A1.2
Per carico verso il basso in genere γG =1.35(sfavorevole), γQ=1.50.
Per carico verso l’alto in genere γG =0.90(favorevole), γQ=0.00.
Va specificata l’altezza dalla superficie della fondazione dell’applicazione del carico.
Tirante in acciaio e spinta passiva del terreno.
Le alte forze orizzontali agenti alla base agiscono verso l’esterno come risultato della flessione nel pilastro dovuta al carico verticale sul tetto.
Questo è assorbito in due modi.
- Tirante in acciaio alla base del pilastro Un tirante gettato nella piastra in calcestruzzo connessa alla base dei pilastri. Questo andrebbe considerato come il metodo più sicuro per assorbire le forze orizzontali alla base dei pilastri.
- Spinta passiva del terreno al lato della fondazione. In questo caso il terreno di riempimento sul lato della fondazione deve essere compattato con cura, in modo che la spinta passiva del terreno sia pienamente operativa. La larghezza trasversale della fondazione By e l’altezza Bh sono usate per calcolare l’area attiva per la spinta passiva del terreno.
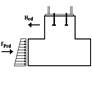
Se si preme il pulsante per il predimensionamento  , le dimensioni della fondazione (se non verificata) sono progettate dal programma in modo che il peso della fondazione sia sufficiente per assorbire le forze di sollevamento. La larghezza By e l’altezza devono anche garantire una spinta passiva del terreno adeguata per assorbire le forze orizzontali alla base verso l’esterno.
, le dimensioni della fondazione (se non verificata) sono progettate dal programma in modo che il peso della fondazione sia sufficiente per assorbire le forze di sollevamento. La larghezza By e l’altezza devono anche garantire una spinta passiva del terreno adeguata per assorbire le forze orizzontali alla base verso l’esterno.
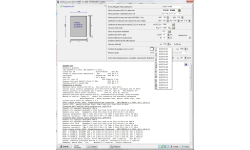
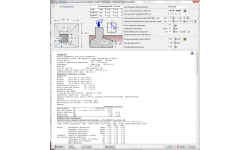
SERBATOI - PISCINE

Il progetto è per Serbatoi rettangolari. La soluzione è per una sezione bidimensionale lungo la dimensione minore (larghezza) del serbatoio.
Le dimensioni di base sono la larghezza del serbatoio B [m] (1), la lunghezza del serbatoio L [m](2), e la profondità del serbatoio H [m]( (3).
Si assume che il serbatoio sia su terreno elastico ed è analizzato con l’analisi a elementi finiti. Le pareti del serbatoio sono suddivise in 2 elementi di trave di lunghezza H/2. Il pavimento del serbatoio è modellato con 16 elementi trave con punti nodali connessi al terreno con molle elastiche. La rigidezza delle molle elastiche è calcolata dal modulo di Winkler della fondazione Ks [kN/m2/m] (4).
Le condizioni di carico includono tutti i casi di carico secondo l’Eurocodice 0, (EQU, STR e GEO) per
- serbatoio vuoto (solo spinta del terreno),
- serbatoio pieno senza spinta del terreno
- serbatoio pieno con spinta del terreno
Il progetto del cemento armato include anche la verifica di esercizio, con apertura delle fessure limite specificato in (5).
DIAGRAMMI DI UTILIZZO - PROGETTO DI UNA TRAVE IN C.A.
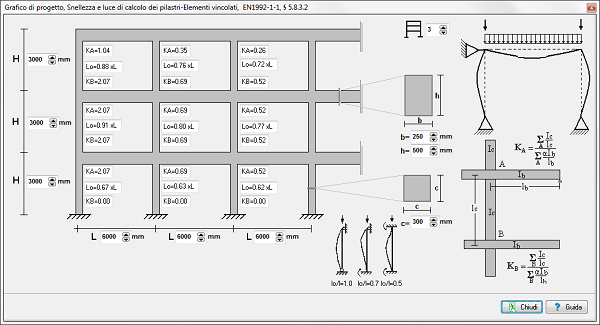
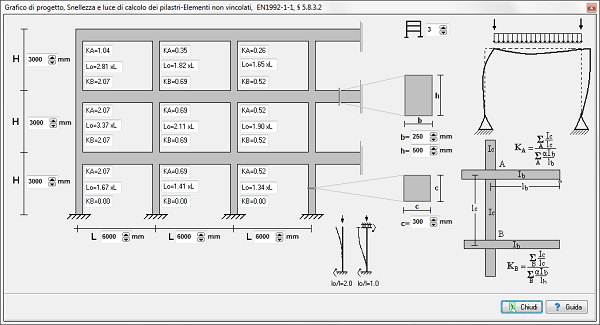
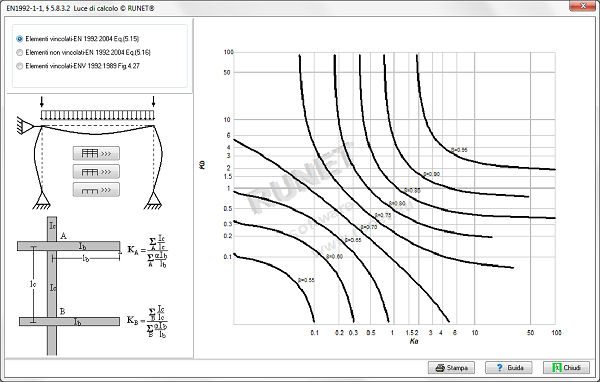
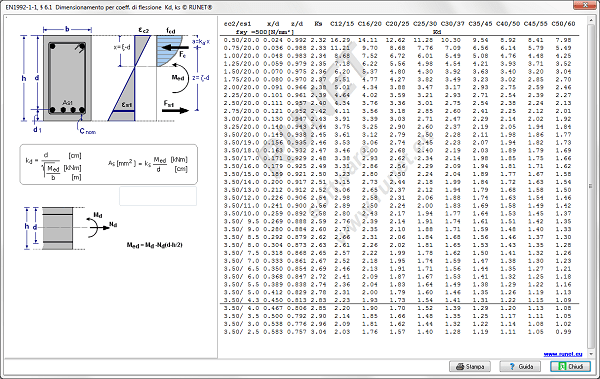
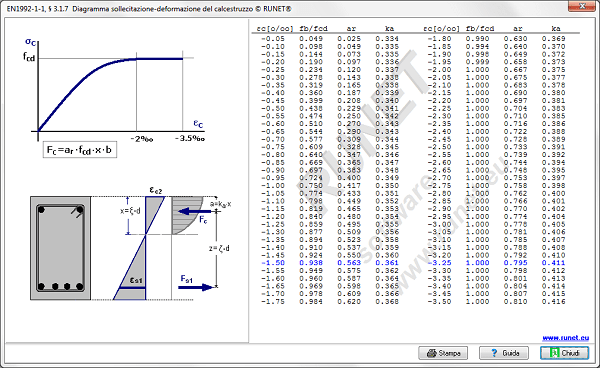
- Tabelle e diagrammi di utilizzo con l’Eurocodice 2: tabelle dei parametri kd e MEd, w per il dimensionamento delle travi inflesse e diagrammi delle lunghezza libera di inflessione dei pilastri.
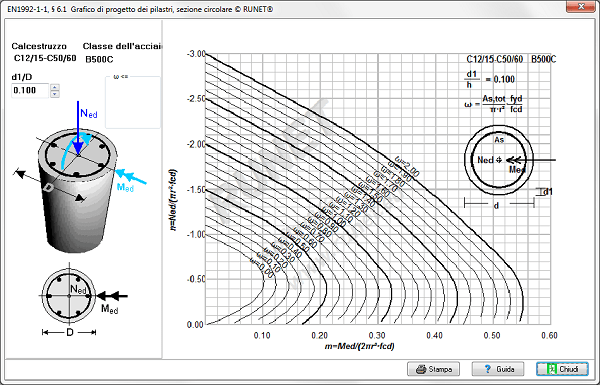
- Diagrammi di utilizzo per il progetto di pilastri a flessione singola e doppia.
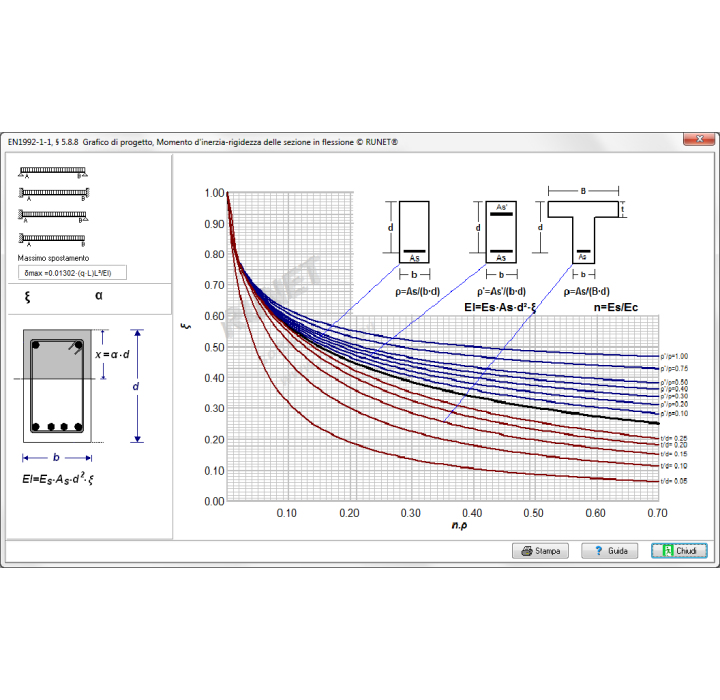
- Diagrammi di utilizzo per la verifica delle frecce
Diagramma di utilizzo per la verifica delle frecce:
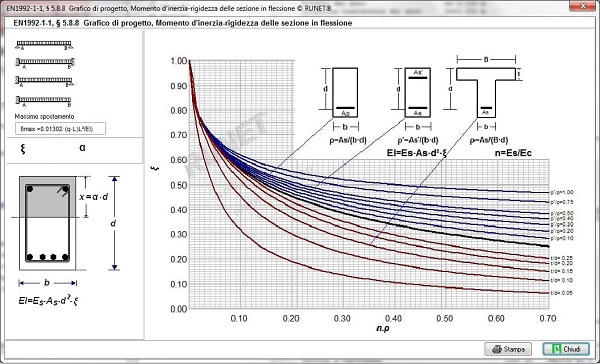
Diagramma di utilizzo per progetto di pilastri a flessione doppia:
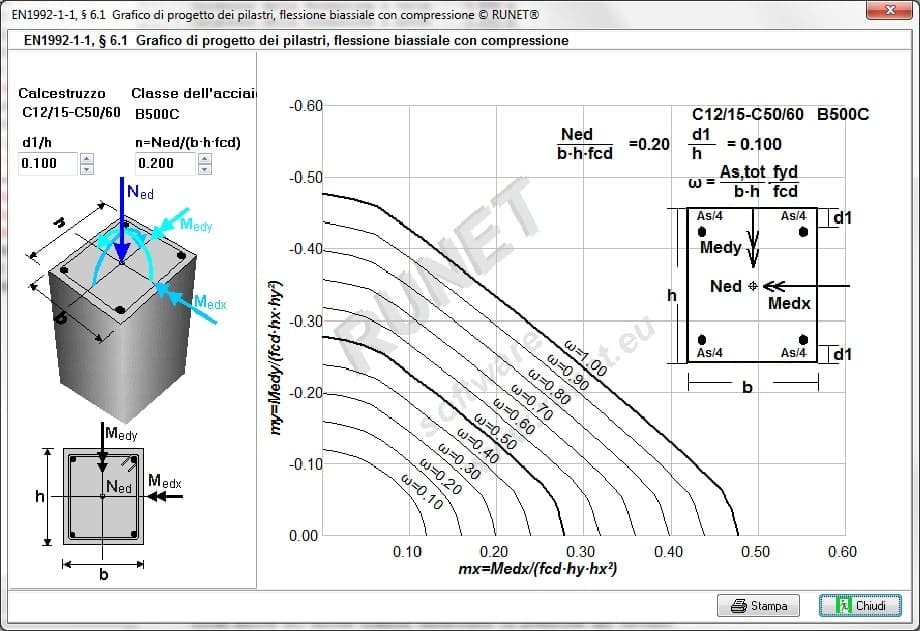
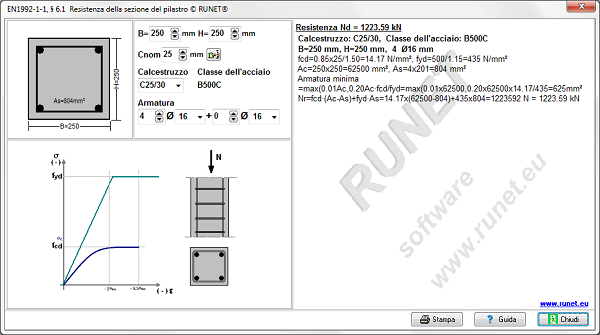
Diagramma di utilizzo per progetto di pilastri a flessione singola:
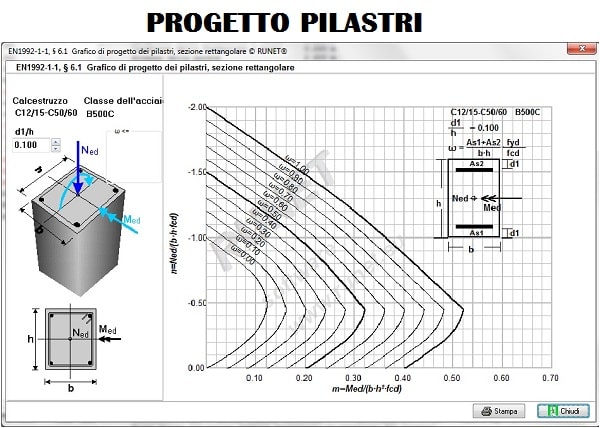
Calcolo degli elementi rinforzati con FRP (polimeri fibro-rinforzati).
Sono inclusi i calcestruzzi normali e alleggeriti.
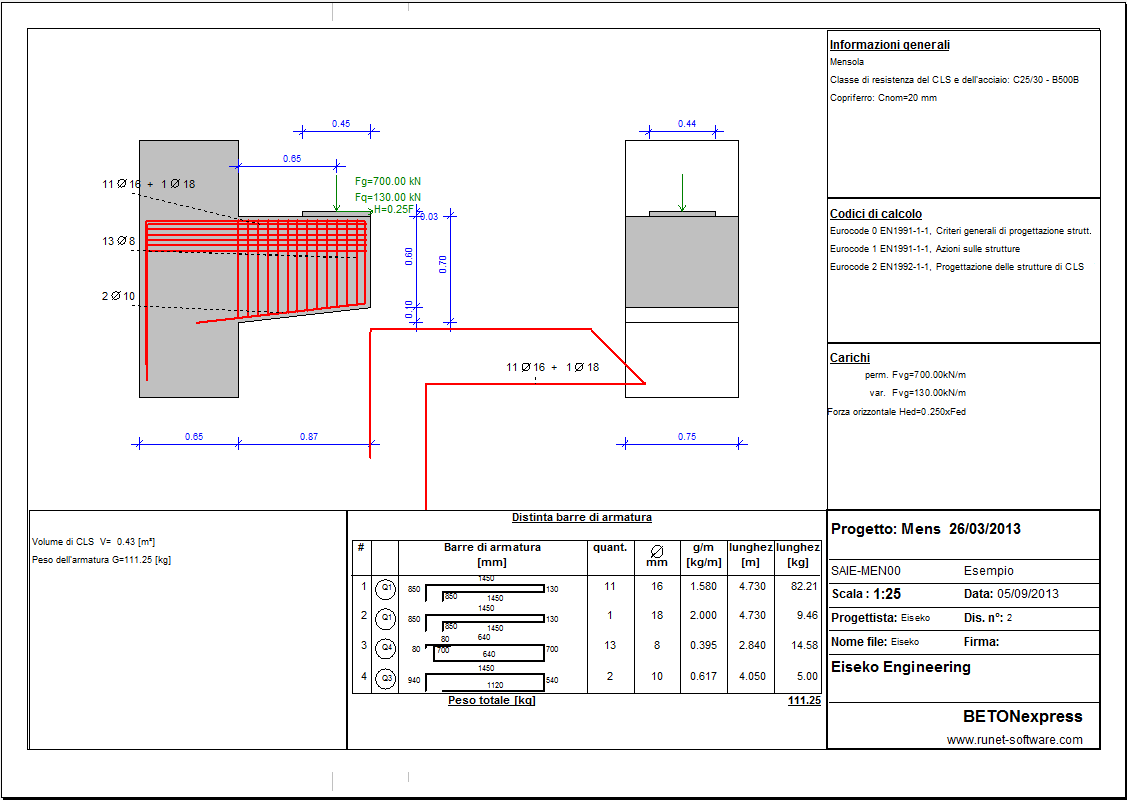
DISEGNI CAD
Generazione automatica dei disegni dettagliati della struttura e dell'armatura. Il programma include un modulo CAD che permette di visualizzare, modificare e salvare i disegni.
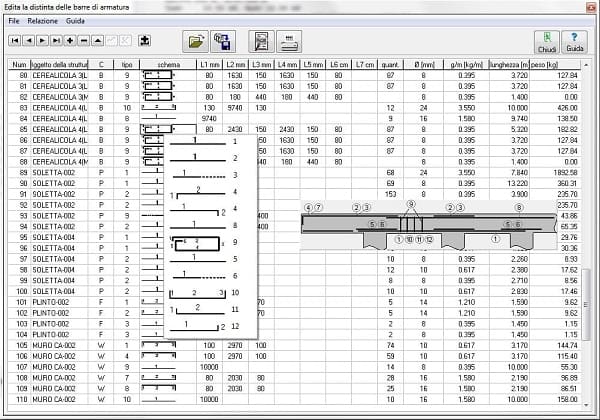
DISTINTA ARMATURE
Distinta dei ferri automatica per i componenti in calcestruzzo progettati. La distinta dei ferri può essere editata con un Editor apposito, incluso nel programma.Le relazioni e le tabelle possono essere esportate in file WORD o PDF.
Tabella delle armature dettagliate:
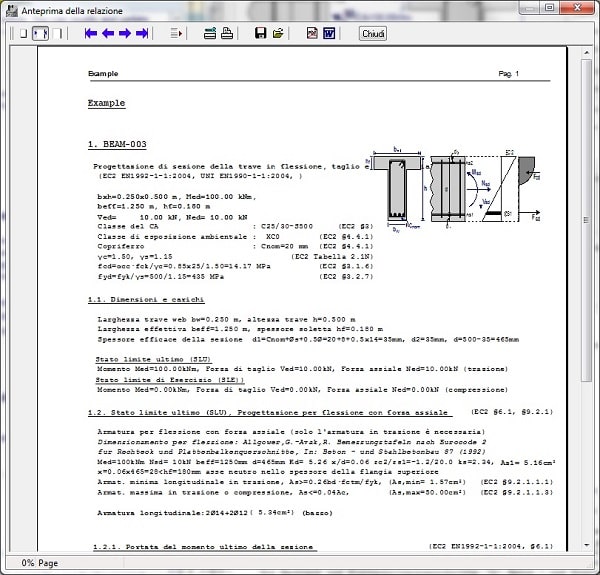
ANTEPRIMA E STAMPA DELLE RELAZIONI
Produzione automatica di una relazione di calcolo dettagliata. Le verifiche cambiano dinamicamente quando l'utente cambia l'input. Presupposizioni e riferimenti alle norme di progettazione sono indicati nelle relazioni di calcolo.
Anteprima completa delle relazioni. Le relazioni sono molto analitiche, mostrano tutti i calcoli eseguiti e i grafici, con i riferimenti ai paragrafi del codice di progetto. Gli errori e le misure inadeguate sono mostrate in rosso.
- Esportazione di tutte le relazioni in formato PDF o Word.
- Esportazione di tutti i disegni CAD in PDF o DXF.
ANNESSI NAZIONALI – PARAMETRI – NORMATIVE DI PROGETTO
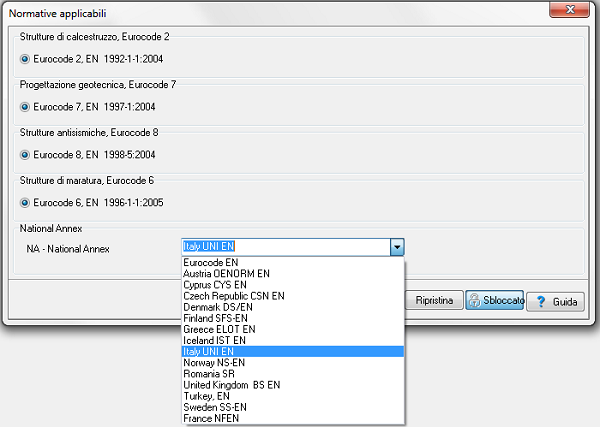
Si possono impostare gli Annessi Nazionali (automaticamente con la scelta della lingua).
I parametri dell’Eurocodice, così come i valori di default, possono essere regolati dall’utente.
MANUALE IN LINEA
Un manuale completo in linea aiuta l’utente per i dati necessari, come per i riferimenti al corrispondente argomento della normativa, e anche per una visione d’insieme della teoria.
- Il manuale è anche in formato PDF e Word (DOC).
STRUMENTI PER L’INGEGNERE
Sono inclusi nel programma vari strumenti utili per l'Ingegnere:
- Conversione di unità di misura
- Calcolo delle aree
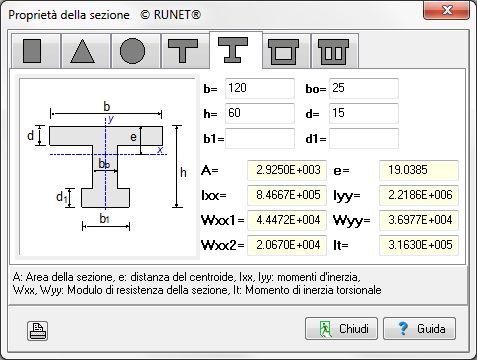
- momenti d'inerzia
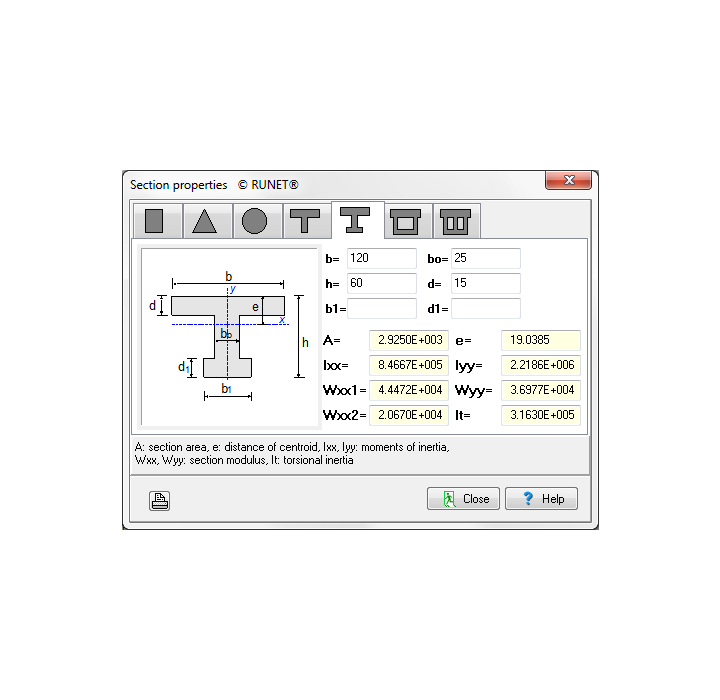
- Proprietà delle sezioni
- sezioni standard dei tondini di acciaio
- Calcolo di profilati laminati
- Strumenti per le armature
- Lunghezza degli ancoraggi
- Coefficienti della pressione sul terreno
ALTRI CALCOLI
RIFERIMENTI
Per il progetto del cemento armato è usato l’Eurocodice 2, per i progetti geotecnici l’Eurocodice 7, per il progetto sismico l’Eurocodice 8 e per i muri a gravità l’Eurocodice 6. In più, nel progetto dei plinti e dei muri di contenimento a gravità, può essere usato il metodo delle tensioni ammissibili.
Eurocodice 0 1990:2002 Criteri generali di progettazione strutturale
Eurocodice 1 EN 1991-1-1:2002 Azioni sulle strutture – Azioni in generale – Pesi per unità di volume, pesi propri e sovraccarichi per gli edifici.
Eurocodice 1 EN 1991-1-2:2002 Azioni sulle strutture - Azioni in generale - Azioni sulle strutture esposte al fuoco
Eurocodice 1 EN 1991-1-3:2003 Azioni sulle strutture– Azioni in generale – Carichi da neve
Eurocodice 1 EN 1991-1-4:2005 Azioni sulle strutture – Azioni in generale – Azioni del vento
Eurocodice 1 EN 1991-1-5:2003 Azioni sulle strutture – Azioni in generale – Azioni termiche
Eurocodice 1 EN 1991-1-6:2005 Azioni sulle strutture – Azioni in generale – Azioni durante la costruzione
Eurocodice 1 EN 1991-1-7:2005 Azioni sulle strutture – Azioni in generale – Azioni eccezionali
Eurocodice 2 EN 1992-1-1:2004 Progettazione delle strutture di calcestruzzo, Regole generali e regole per gli edifici
Eurocodice 2 EN 1992-1-2:2004 Progettazione delle strutture di calcestruzzo, Regole generali - Progettazione strutturale contro l’incendio
Eurocodice 3 EN 1993-1-1:2005 Progettazione delle strutture di acciaio
Eurocodice 4 EN 1994-1-1:2004 Progettazione delle strutture composte acciaio-calcestruzzo, Regole generali e regole per gli edifici
Eurocodice 5 EN 1995-1-1:2003 Progettazione delle strutture in legno– General – Regole generali - Regole comuni e regole per gli edifici
Eurocodice 5 EN 1995-1-2:2003 Progettazione delle strutture in legno – Regole generali - Progettazione strutturale contro l'incendio
Eurocodice 6 EN 1996-1-1:2005 Progettazione delle strutture in muratura, Regole generali per strutture di muratura armata e non armata
Eurocodice 6 EN 1996-1-2:2005 Progettazione delle strutture in muratura, Regole generali - Progettazione strutturale contro l'incendio
Eurocodice 7 EN 1997-1:2004 Progettazione geotecnica – Regole generali
Eurocodice 8 EN 1998-1:2004 Progettazione delle strutture per la resistenza sismica, Regole generali, azioni sismiche e regole per gli edifici
Eurocodice 8 EN 1998-5:2004 Progettazione delle strutture per la resistenza sismica, Fondazioni, strutture di contenimento ed aspetti geotecnici
Eurocodice 9 EN 1999-1-1 Progettazione delle strutture in alluminio, Regole generali
Eurocodice 1 (EC1) ENV 1991 Basi della progettazione e Azioni sulle strutture
Eurocodice 2 (EC2) ENV 1992 Progettazione delle strutture di calcestruzzo.
Eurocodice 6 (EC6) ENV 1996 Progettazione delle strutture in muratura.
Eurocodice 7 (EC7) ENV 1997 Progettazione geotecnica.
Eurocodice 8 (EC8) " Progettazione delle strutture per la resistenza sismica, Parte 5, Fondazioni, strutture di contenimento ed aspetti geotecnici" Draft, January 1991.
Bares R. and Massonet Ch., "Analysis of beam grids and orthotropic plates", Frederic Ungar Publishing Co. Inc., New York, 1968,
Marcus H., "Die vereinfachte Barechnung biegsamer Platten", 2nd ed., Springer-Verlag, Berlin, 1929.
Czerny, F., "Tafeln für vierseitig gelagerte Rechteckplatten", Beton Kalender, Vol1, W. Ernst und Sohn, Berlin, 1965, pp 233-261.
Mononobe N, "Earthquake proof construction of masonry dams", Proceedings, World Engineering Conference, Volume 9, p275, 1929.
Okabe S "General Theory of Earth Pressure", Journal of Japanese Society of Civil Engineers, volume 12, No 1, 1926.
Gipson, R. F. "Principles of Composite Material Mechanics", McGraw-Hill, New York, 1994
IMPOSTAZIONI NAD:
Il programma è basato sugli Eurocodici strutturali. L’applicazione, così come i parametri degli Eurocodici, possono differire da nazione a nazione.
E’ consigliabile consultare i NAD, che definiscono i parametri, gli standard di supporto e forniscono una linea guida nazionale sull’applicazione degli Eurocodici.
Dopo l’installazione del programma, l’utente deve selezionare gli Annessi Nazionali della propria area. Se necessario si possono anche aggiustare vari parametri come le costanti dei materiali, i coefficienti di sicurezza, i valori di default e i requisiti minimi di armatura.
Parametri
Regole di calcolo. Si può scegliere il codice di progetto che si vuole utilizzare (selezionare l’Eurocodice o la normativa nazionale per il progetto del calcestruzzo, Eurocodice 7 o tensioni ammissibili per il progetto dei plinti e la sismica).
Classe del CA. Si può selezionare la classe di default del calcestruzzo e la classe di default dell’armatura.
Normative applicabili Si possono selezionare gli Annessi Nazionali da applicare per il progetto.
Calcestruzzo armato, Caratteristiche dell’acciaio, Tipo di terreno, Materiali fibro-rinforzati. Si possono adattare le proprietà caratteristiche dei materiali. E’ consigliabile consultare il NAD degli Eurocodici 0, 1, 2, 6, 7, 8.
Parametri del calcestruzzo armato, Parametri delle fondazioni, Parametri dei muri di contenimento. Si possono selezionare i valori di default per vari parametri di progetto.
Regole di calcolo
Opzioni:
Calcestruzzo armato
- Secondo l’Eurocodice 2
- Normativa nazionale (se disponibile)
Progettazione Geotecnica
- Progetto agli Stati Limite Ultimi, secondo l’Eurocodice 7
- Progetto usando gli Sforzi di Esercizio (tensioni ammissibili)
Strutture in muratura
- Progetto agli Stati Limite Ultimi, secondo l’Eurocodice 6
- Progetto usando gli Sforzi di Esercizio (tensioni ammissibili)
Progettazione sismica
- Con Progettazione sismica (per plinti e per muri di contenimento), secondo l’Eurocodice 8
- Senza progettazione sismica.
Eurocodici:
Eurocodice 0 EN 1990:2002, Combinazione di carichi
Secondo l’Eurocodice EN 1990:2002 i valori di progetto per le azioni dovrebbero essere combinati come
SgG,j Gk,j +gQ,1 Qk,1+SgQ,i yQ,i Qki
Fattori per combinazioni permanenti e accidentali, Eurocodice 0 Annesso A1.
Valori comuni per questi fattori sono gG=1.35, and gQ=1.50.
Eurocodice 2, progetto calcestruzzo
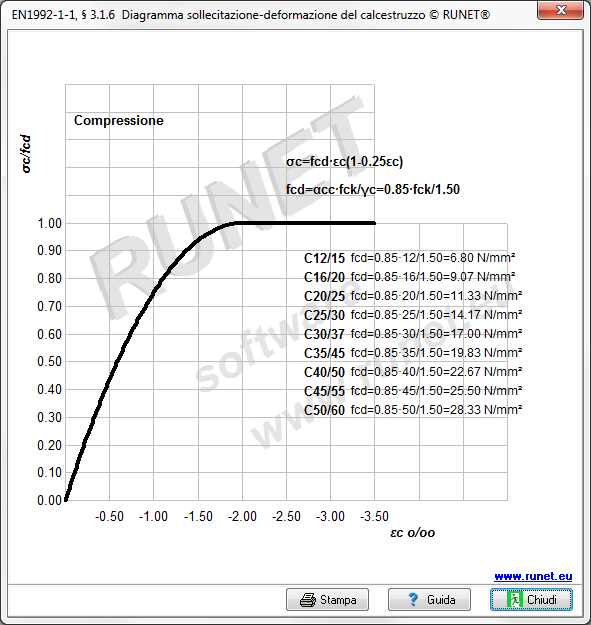
Calcestruzzo (Eurocodice 2 §3.1)
La classe di resistenza del calcestruzzo è classificata dalla resistenza cilindrica o cubica Eurocodice 2 §3.1.2.4.
fck: Resistenza caratt. Cilindrica a 28gg
fck,c: Resistenza caratt. cubica
fctm: Resistenza media Traz. assiale
fctk0.05: resistenza a trazione minima
fctm0.95: resistenza a trazione max
fct,fl: resistenza a trazione e flessione
fvck: resistenza a taglio
Ec: modulo di elasticità
Gc: modulo a taglio
w: peso specifico
Il coeff. di Poisson può essere preso=0.20
Coefficiente di espansione termica 0.00001 /°C
Viscosità e ritiro del calcestruzzo
Densità per calcestruzzo a peso normale tra 2000 e 2888 kg/m³ (valore comune 2400 kg/m³).
Acciaio armatura Eurocodice 2, §3.2
L’acciaio dell’armatura è classificato secondo il valore caratteristico della tensione di snervamento fyk.
fyk: valore caratteristico della tensione di snervamento
ftk,c: resistenza a trazione
Es: modulo di elasticità
euk: allungamento per carico massimo.
L: lunghezza barra
Valore medio della densità 7885 kg/m³
Coefficiente di espansione termica 0.00001 /°C
Valore caratteristico duttilità
Alta duttilità euk>5% valore di (ft/fy)k>1.08
Duttilità Normale euk>2.5%, valore di (ft/fy)k>1.05
Copriferro, Eurocodice 2 §2.4.1.3.3
Si può selezionare il copriferro dalle condizioni ambientali secondo la tabella 4.3N e 4.4N
Copriferro è la distanza tra la superficie esterna dell’armatura e la superficie più vicina del calcestruzzo. Il copriferro minimo richiesto a seconda dalle condizioni ambientali è dato in Eurocodice 2 §4.4.1.2.
In generale:
Il copriferro minimo per ambiente secco e per l’interno degli edifici è 15 mm, per ambiente umido senza gelo 20 mm e per ambiente umido con gelo 25 mm. Per ambienti più aggressivi come umidi con gelo e sali anti-gelo o ambiente marino, per componenti in calcestruzzo interni ed esterni il copriferro minimo è 40 mm.
Altre referenze:
Stati Limite Ultimi per flessione Eurocodice 2 § 6.1
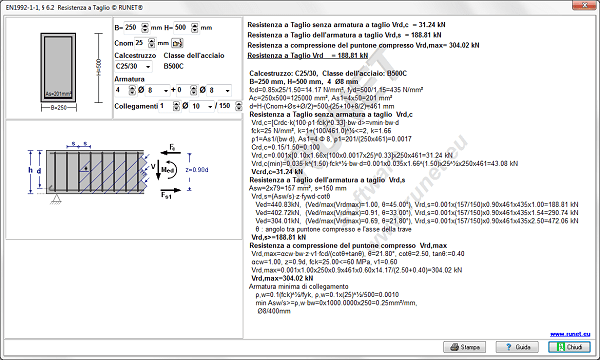
Taglio Eurocodice 2 § 6.2
Punzonamento, Eurocodice 2 § 6.4
Torsione Eurocodice 2 § 6.3.
Coefficienti di viscosità e ritiro
Il coefficiente di viscosità a tempo infinito è usato nei calcoli degli spostamenti e nelle verifiche sull’apertura delle fessure negli Stati limite di Esercizio (SLE). Si può calcolare il coefficiente di viscosità dai parametri ambientali e dalle dimensioni della sezione secondo EN 1992-1-1:2004, par 3.1.4. e Annesso B.
Eurocodice 7, Progetto geotecnico
Eurocodice 7, EN 1997-1:2004, Progetto geotecnico – Regole Generali, Annesso A, per casi limite EQU STR e GEO.
Fattori parziali per la verifica allo stato limite di equilibrio (EQU), agli stati limite strutturali (STR) e geotecnica (GEO):
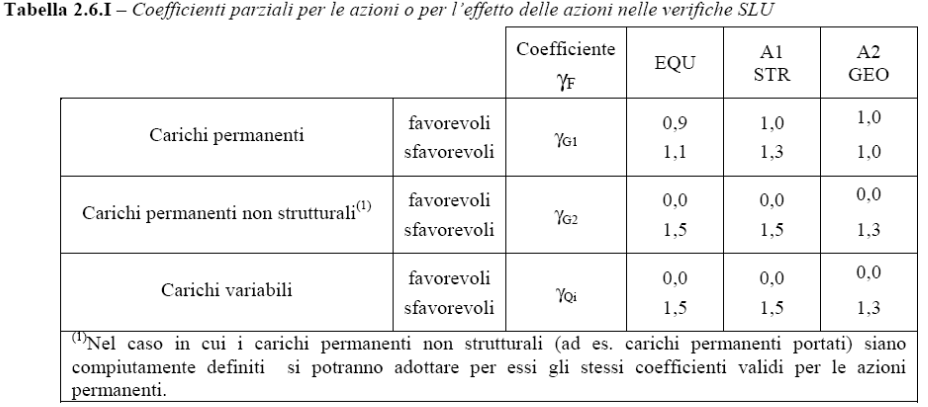
Eurocodice 8, Progettazione sismica
La progettazione sismica è inclusa nel calcolo dei plinti e dei muri di contenimento, Eurocodice 8 Parte 5.
Nei plinti:
Specificare il carico aggiuntivo verticale e i momenti Mxx e Myy sulla sommità del plinto dovuti al sisma.
Due combinazioni di carichi di progetto aggiuntive sono trattate secondo l’Eurocodice 8.
Carichi -2 P.pr. + perm. + y2xAccid + Sismico x-x,
Carichi -3 P.pr. + perm. + y2xAccid + Sismico y-y
Una restrizione nella progettazione sismica è data dal rapporto (area plinto efficace)/(area plinto)< coefficiente, definito in [Parametri/Parametri dei muri di contenimento]. Questo coefficiente ha valore di default 0.50.
Nei muri di contenimento:
Specificare l’accelerazione al suolo di progetto a. L’accelerazione orizzontale sismica è presa ah=axg (dove g è l’accelerazione di gravità).
I coefficienti sismici finali orizzontali e verticali che riguardano tutte le masse sono presi secondo l’Eurocodice 8 Parte 5, § 7.3.2: kh=a/r, e kv=cxkh. I coefficienti r e c sono definiti in [Parametri/Parametri dei muri di contenimento], e i valori usuali sono r=1.50, c=0.50.
Nei carichi sismici, l’effetto della forza passiva del terreno è presa in considerazione con un fattore ridotto definito in [Parametri/Parametri dei muri di contenimento] e ha valore usuale 0.50.
Una restrizione nella progettazione sismica il rapporto (area plinto efficace)/(area plinto)< coefficiente, definito in [Parametri/Parametri dei muri di contenimento]. Questo coefficiente ha valore di default 0.50.
Una restrizione aggiuntiva è che secondo l’Eurocodice 8 Parte 5, § 7.3.2 3 (6) la resistenza a taglio tra suolo e muro dev’essere minore del rapporto (generalmente 2/3=0.67) della resistenza a taglio del suolo. Questo rapporto è definito in [Parametri/Parametri dei muri di contenimento].
Le forze sismiche aggiuntive, dovute alla spinta del terreno attiva, sono calcolate secondo l’Eurocodice 8 Parte 5, Annesso E, usando la formula di Mononobe-Okabe [ref.]. Perciò la spinta del terreno attiva aumentata con il carico sismico è calcolata come:

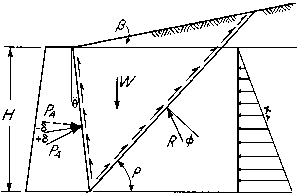
In aggiunta le forze orizzontali e verticali agiscono nel baricentro del muro a causa della sua massa. Queste forze sono uguali a Fh=kh.W e Fv=kv.W. Dove kh e kv sono i coefficienti sismici orizzontali e verticali.
Unità
Le unità usate nel programma sono quelle del SI (Sistema Internazionale delle unità di misura). Le unità di ogni dato di input sono indicate vicino alla casella di testo per l’introduzione del dato. Anche nella relazione sono indicate tutte le unità di misura.
Unità usate nel programma:
lunghezze [m]
forze [kN]
momenti [kNm]
tensioni [N/mm²] = [GPa]
carichi concentrati [kN]
carichi distribuiti [kN/m²]
carichi lineari [kN/m]
diametro armature [mm]
copriferro [mm]
Si possono modificare le unità delle armature nella relazione.
Esempi BETONexpress: puoi scaricare gratuitamente questi esempi di calcolo e verificarli sia con la versione FREE-TRIAL che con la versione FULL di BETONexpress.
Esempio SOLETTE (17.5 MB)
Esempio TRAVI (10 MB)
Esempio PILASTRI (8 MB)
Esempio PLINTI (2.96 MB)
Esempio MURI (12.8 MB)
Esempio ELEMENTI TOZZI (2.2 MB)
Esempi input dati
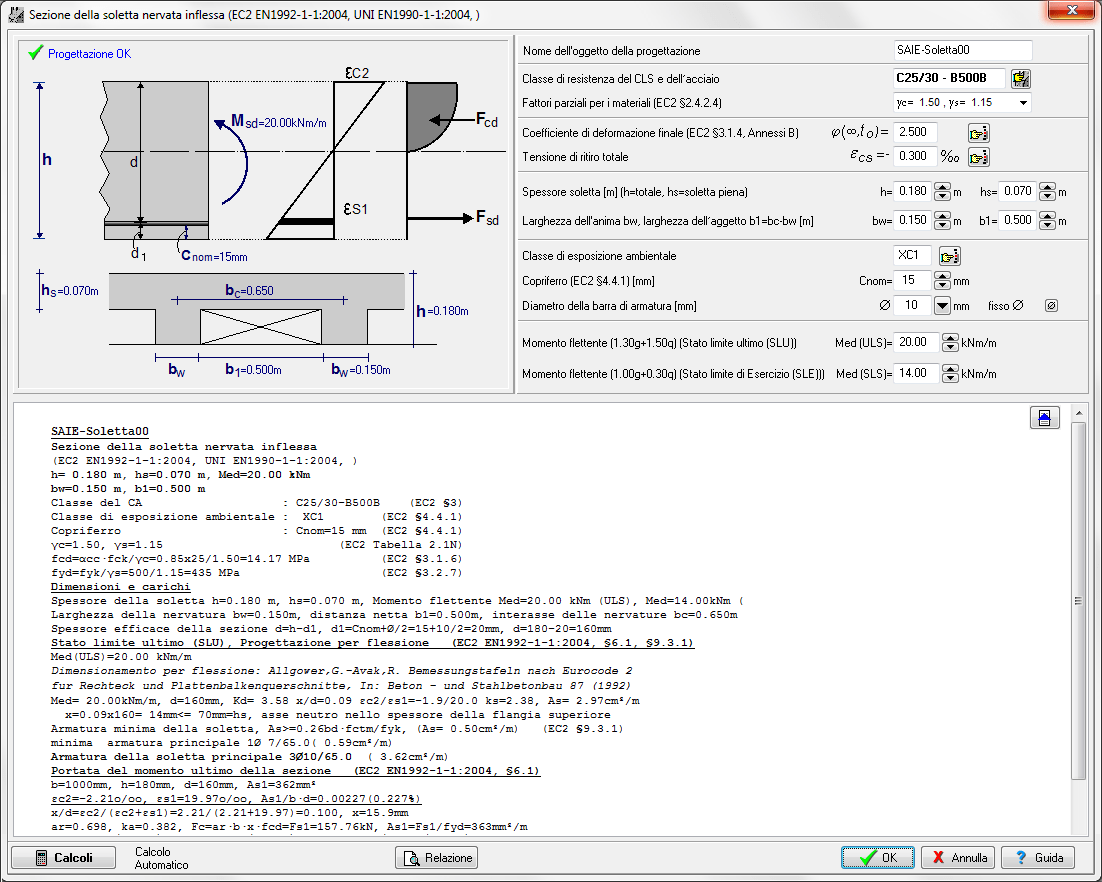
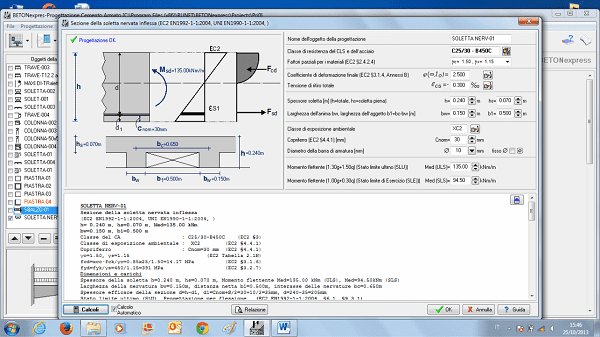
sezione di una soletta nervata inflessa
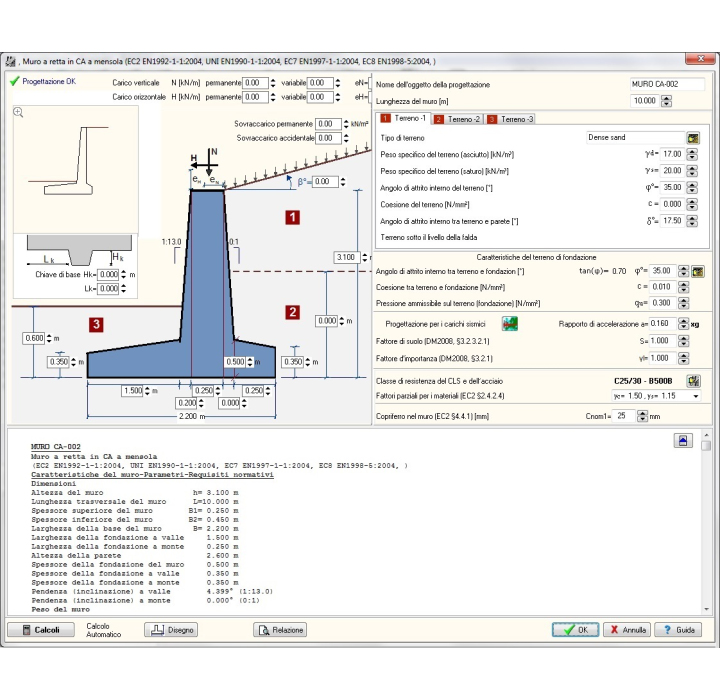
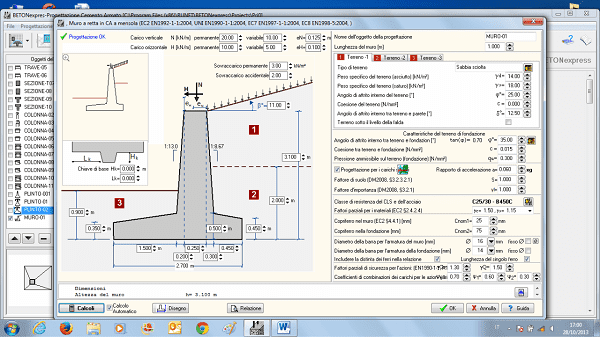
muro a retta in ca a mensola
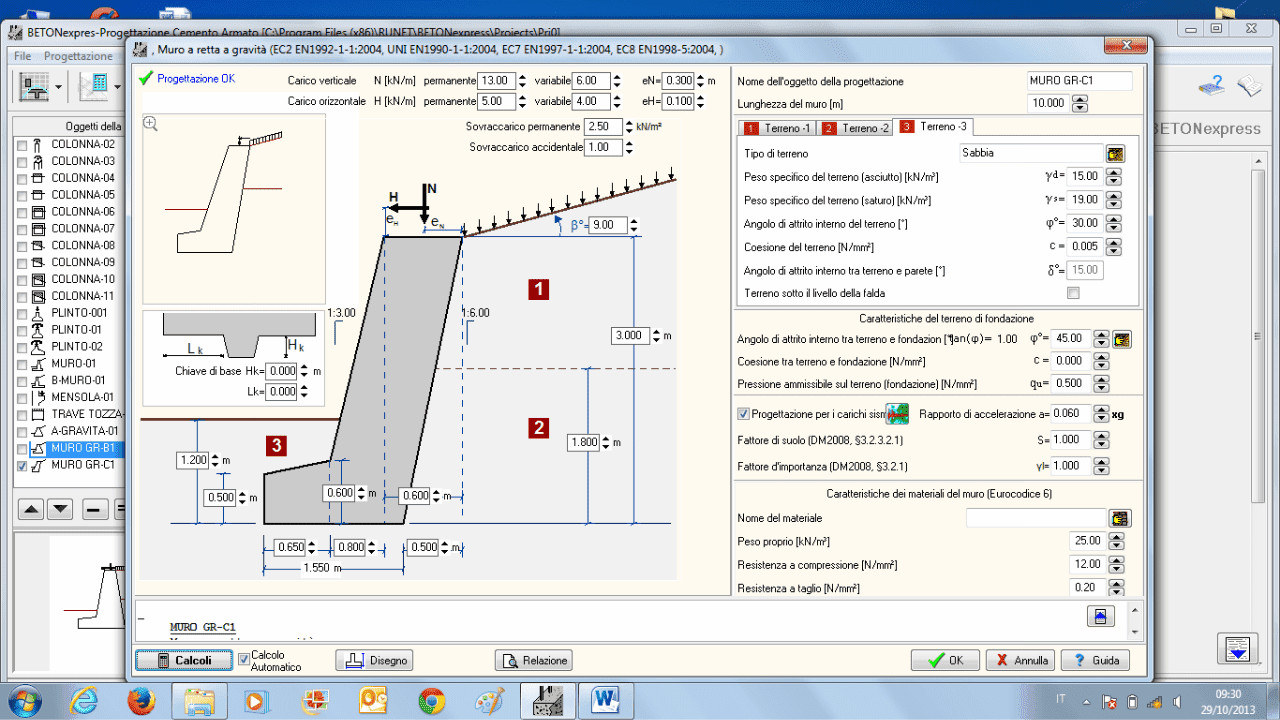
muro a retta a gravità
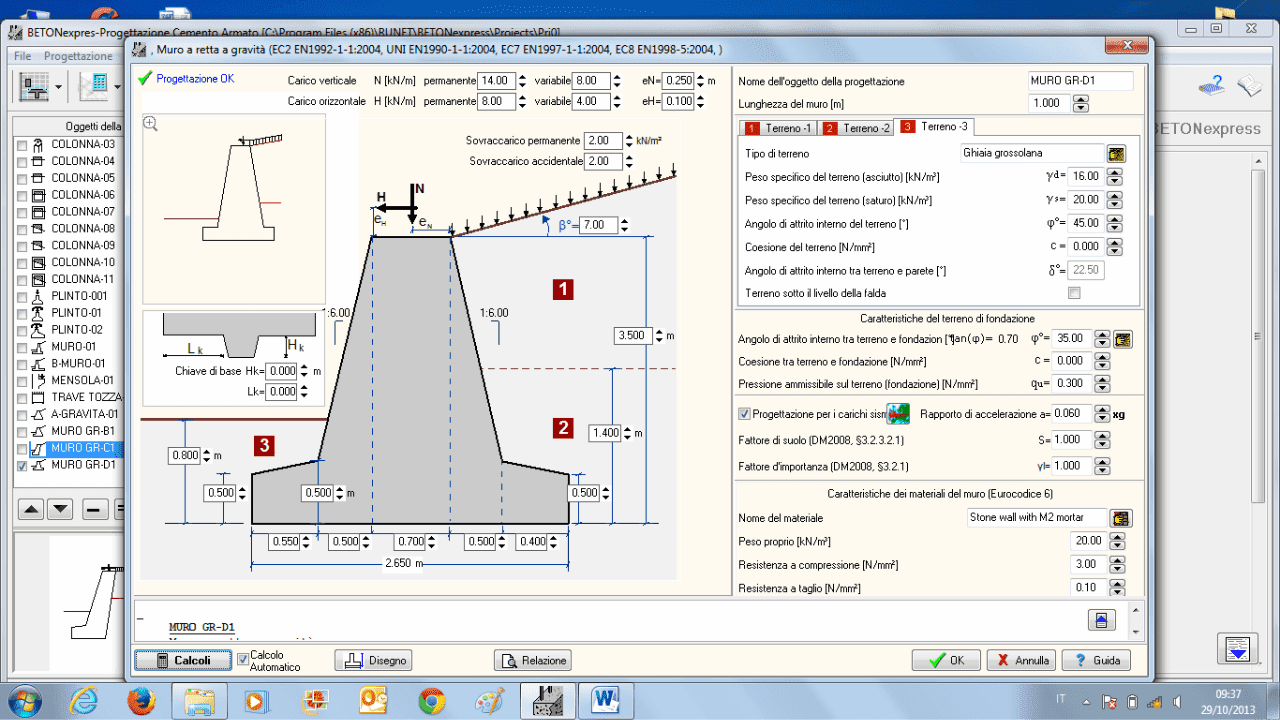
mensola
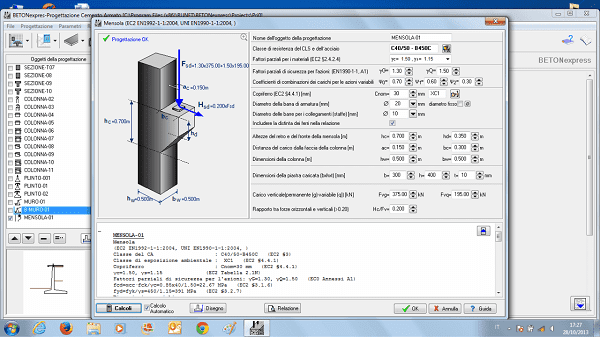
doppia flessione del singolo pilastro
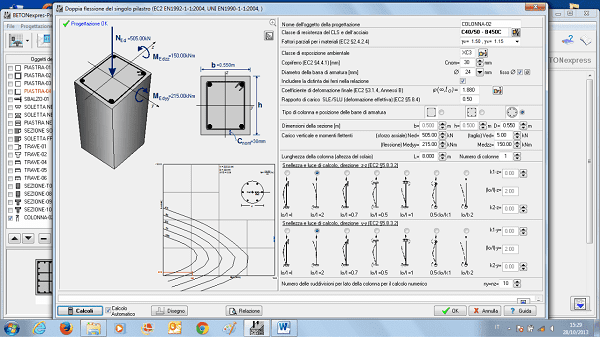
colonna isolata
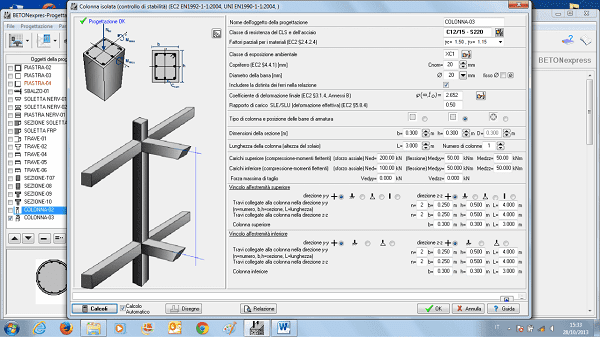
resistenza della colonna con FRP
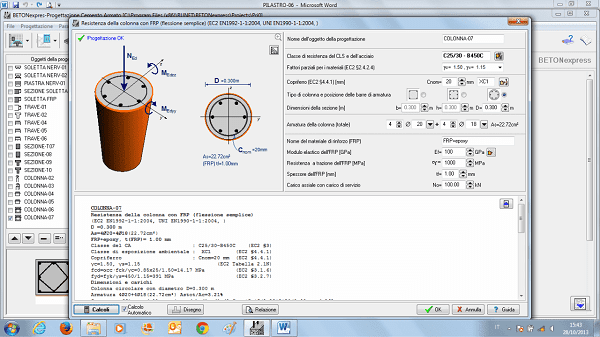
plinto asimmetrico con carico eccentrico
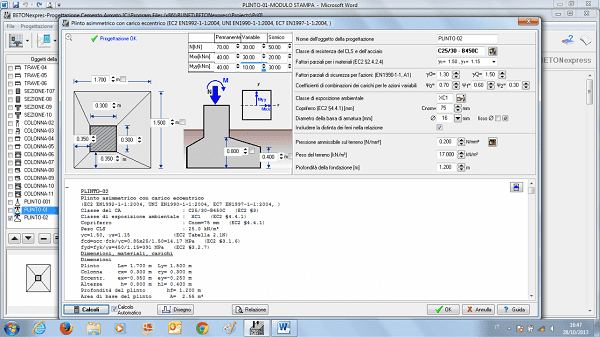
sezione della soletta inflessa
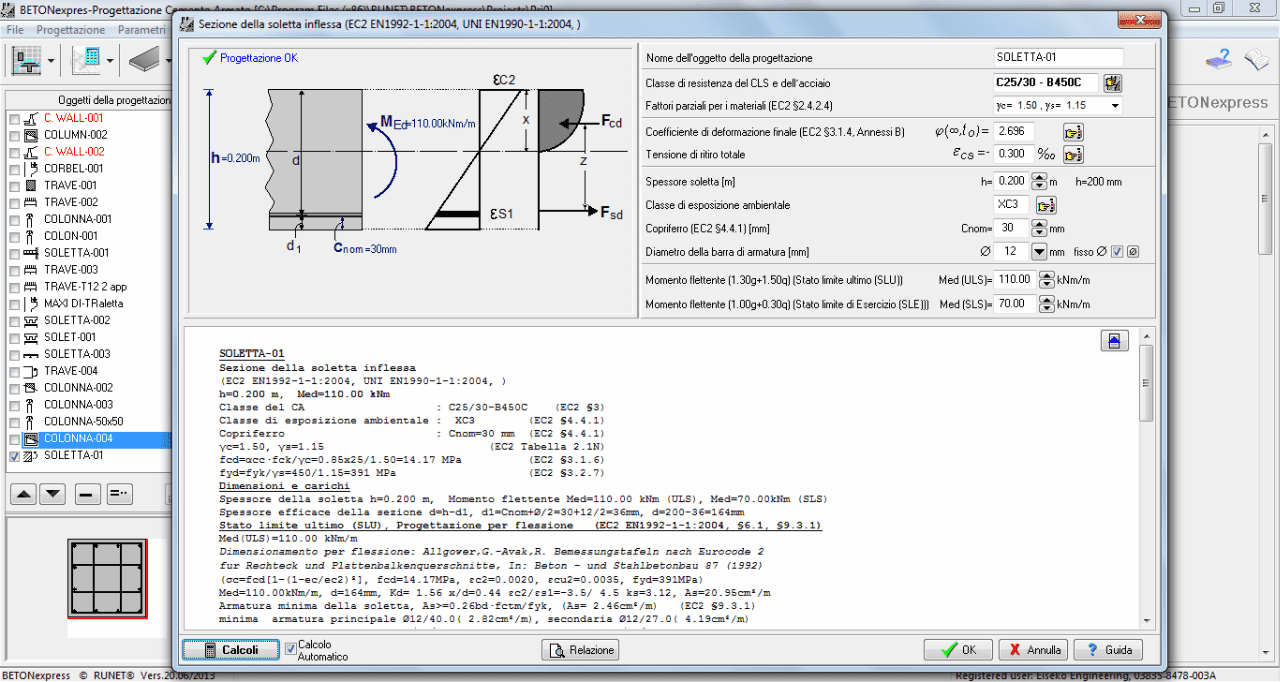
trave semplicemente appoggiata con carico misto
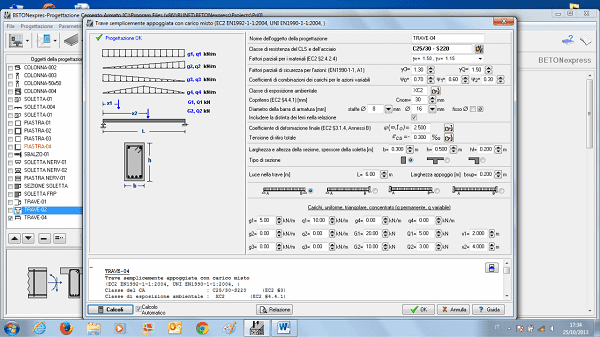
trave tozza
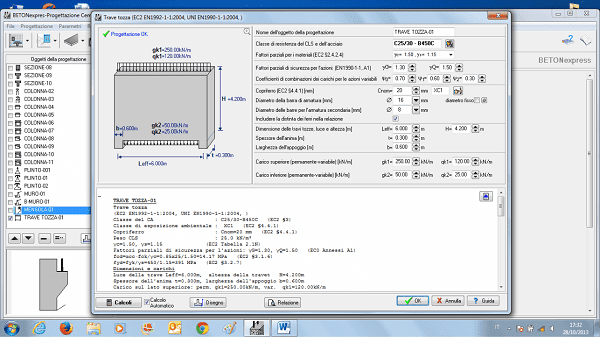
Istruzioni per aggiornare il programma BETONexpress e tutti gli altri software Runet (WOODexpress, STEELexpress, EUROCODEexpress, SteelPortalFrame etc.)
Lanciare il programma, andare nel menù in alto "Aggiornamento" e cliccare dove indicato in rosso:
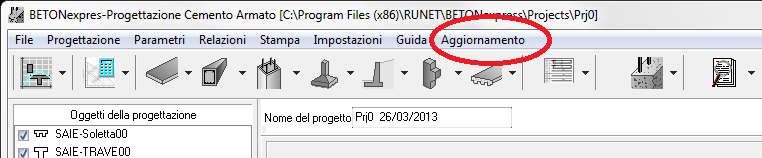
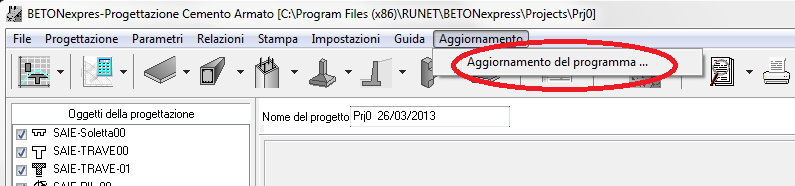
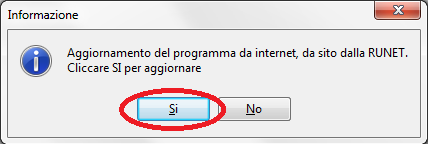
I programmi vengono continuamente aggiornati in base al nuovo ambiente Windows e all'Eurocodice o agli standard su cui si basa Per le nuove versioni è possibile eseguire l'aggiornamento scaricando la nuova versione dal menu principale / Aggiorna.
La licenza è permanente e gli aggiornamenti sono gratuiti, in genere viene rilasciata una nuova versione ogni 2/3 mesi. Solo nel caso in cui vengano effettuate aggiunte importanti sul tipo di elementi da calcolare o sulle normative, viene richiesto un costo per l’aggiornamento (circa il 20%-30% del costo del programma). Per capirci, dal 2013, questo è avvenuto solo 1 volta sul BETONexpress perché sono stati raddoppiati gli elementi calcolabili, mentre ad esempio l’aggiornamento per nuove normative italiane NTC2018 è stato gratuito. A nostra discrezione.
No, non ci sono canoni di manutenzione e gli aggiornamenti sono generalmente gratuiti.
La licenza è permanente e gli aggiornamenti sono gratuiti, in genere viene rilasciata una nuova versione ogni 2/3 mesi. Solo nel caso in cui vengano effettuate aggiunte importanti sul tipo di elementi da calcolare o sulle normative, viene richiesto un costo per l’aggiornamento (circa il 20%-30% del costo del programma). Per capirci, dal 2013, questo è avvenuto solo 1 volta sul BETONexpress perché sono stati raddoppiati gli elementi calcolabili, mentre ad esempio l’aggiornamento per nuove normative italiane NTC2018 è stato gratuito. A nostra discrzione.
Richiesta codice di attivazione
Dopo l'installazione, la prima volta che esegui il programma ti verrà chiesto un codice di attivazione.
Basta premere il pulsante [e-mail a RUNET] e presto riceverai il codice di attivazione via e-mail.
Se l'antivirus blocca il messaggio, digita i numeri del codice del programma in una normale e-mail all'indirizzo indicato nella finestra di attivazione oppure compila i numeri nei campi vuoti qui sotto e inviaci il messaggio.
No, il software ha solo protezione software.
La finestra di dialogo Imposta stampante non viene visualizzata perché la stampante predefinita di Windows non esiste. Di solito ciò accade in vecchie versioni di Windows quando la stampante predefinita è una stampante Netware e non si è connessi a Netware o la stampante non è accesa.
Per risolvere il problema, collegare la stampante o modificare la stampante Windows predefinita.
Da [Impostazione relazione/ Caratteri, paragrafi ..] in basso si imposta la dimensione del testo nei grafici.
Per modificare la relazione di calcolo a piacimento è possibile esportare la relazione in un documento RTF. Aprendo poi il documento esportato con qualsiasi editor di testi puoi eseguire le modifiche desiderate.
Affinché il programma utilizzi il diametro dell'armatura specificato dall'utente, è necessario selezionare la casella accanto al diametro specificato. In caso contrario, il programma seleziona un diametro, attorno al diametro specificato, ottimizzando il rinforzo.
Oppure può essere impostato il diametro minimo superiore a quello indicato, nei parametri per il rinforzo del calcestruzzo. Fare clic su Parametri / Cemento armato e modificare il limite inferiore della barra di rinforzo.
Questo succede se perché Windows non ha il supporto per caratteri greci installato. A seconda dell'installazione di Windows, i simboli matematici greci possono o meno apparire correttamente. Puoi aggiungere il supporto per la lingua greca in Windows: Vai in [Impostazioni / Pannello di controllo / Opzioni internazionali e della lingua / Avanzate]. Altrimenti vai al menu File / Supporto caratteri greci e scegli la tua lingua senza supporto per simboli matematici. Quindi i simboli matematici appariranno esplicitamente, come phi, alpha, beta ecc.
Quando provo a visualizzare l'anteprima della relazione, viene visualizzato il messaggio "Errore stampante ...".
Per visualizzare l'anteprima della relazione, è necessario che nel sistema sia presente una stampante valida. Di solito ciò accade in vecchie versioni di Windows quando la stampante predefinita è una stampante Netware e non si è connessi a Netware o la stampante non è accesa. Per risolvere il problema, collegare la stampante o modificare la stampante Windows predefinita.
Da Impostazione Relazione / Varie impostare i vari rientri.
BETONexpress FREE Download
Per favore compila il modulo sottostante e ti invieremo una mail con il link per scaricare la VERSIONE DEMO del software e tutte le istruzioni all'indirizzo email inserito.
Richiesta informazioni
Compila il modulo sottostante ed inviaci la tua richiesta, il nostro staff risponderà nel minor tempo possibile all'indirizzo email inserito.
News, eventi e promozioni
IDEA STATICA - RILASCIATA LA NUOVA VERSIONE 23.1
Rilasciata la nuova versione IDEA StatiCa 23.1 ►►►Leggi le Release…
FIERA SED | CASERTA | 11 -13 Maggio 2023
Saremo presenti al SED 2023 che si terrà a CASERTA dall'11 al 13 Maggio. Eiseko ti permetterà di partecipare a…
DISPONIBILE IL NUOVO LINK TRA ENEXSYS E IDEA STATICA
Disponibile il plugin della NextFEM per esportare nodi e membrature da WinStrand (Enexsys) verso IDEA StatiCa Connection e Member:…
IDEA STATICA - RILASCIATA LA NUOVA VERSIONE 22.0
Rilasciata la nuova versione IDEA StatiCa 22.0 ►►►Leggi la…

 CYPE Architecture: Software Bim gratuito
CYPE Architecture: Software Bim gratuito